
Seeking the best solution: Mathematical optimization with Mosek
The same problem may have multiple solutions, but the question is: which one is the most appropriate? From a quantitative perspective, the “optimum” is the one that outperforms all other alternatives.
However, the best choice depends on the context (variables) and available options, making decision-making more complex. Mathematical tools are available to create a concrete and measurable framework for addressing these problems. By utilizing data to guide our decisions, we can minimize uncertainty and guarantee that we base our choices on solid evidence.
In mathematics and engineering, optimization aims to maximize or minimize an objective function. This function describes a specific phenomenon or process, helping to enhance efficiency, cut costs, or improve performance based on the given problem’s requirements.
An optimization problem involves finding the optimal value for one or more variables to either maximize or minimize the objective function, which is denoted as f(x) and depends on a set of variables. In this process, the variables are not entirely free; they are bound by constraints that restrict the values they can take, such as equality or inequality constraints.
Optimization problems: types of constraints
Inequality constraints, represented as g(x) ≤ 0, constrain variables to ensure they do not exceed specific values or limits. For instance, in a production scenario, this could indicate that the quantity produced must not surpass the factory’s capacity.
On the other hand, equality constraints, represented as h(x) = 0, require that the variables meet an exact condition. For example, in a budget, the sum of expenditures must equal the available income. The goal is to determine the values of x that optimize the function f(x) while satisfying both inequalities and equalities, ensuring a feasible and optimal solution.
Choosing an optimization tool: competitor comparison and benchmarking
In the mathematical optimization market, tools such as Gurobi, CPLEX, Xpress, Mosek, and SCIP are widely recognized for solving complex problems, each with specific strengths. Gurobi is known for its speed in solving problems with integer constraints (MIP), although it sometimes sacrifices solution quality.
The CPLEX optimization software is highly effective for solving linear and large-scale problems. However, it may encounter challenges when dealing with more complex or nonlinear structures. Xpress and SCIP are both widely used in academic settings. Xpress is particularly adept at handling both linear and nonlinear problems, while SCIP is highly regarded for its flexibility in combinatorial optimization.
Mosek is known for being a highly effective tool for solving optimization problems that include multiple complex constraints and large-scale models. While it may take longer to analyze each possible solution compared to Gurobi, Mosek makes up for this with its ability to concentrate on the most promising regions of the search space. These are the areas where high-quality solutions are most likely to be found.
This approach allows Mosek to avoid spending resources exploring solutions that are unlikely helpful, making the process more efficient in the long run. This quality makes it a reliable tool for applications that require a delicate balance between accuracy and efficiency, especially in contexts where the quality of the solution cannot be compromised. After comparing these features with those of other optimizers, we chose Mosek.
Getting to know Mosek
Mosek is a mathematical optimization software designed to solve various problems, including linear, nonlinear, quadratic, and conic problems. Its primary advantage is its capacity to manage substantial and intricate problems effectively. In addition, it provides advanced tools for using both inequality and equality constraints.
There are three ways or interfaces to use this tool:
- Matrix-Oriented Interface (Optimizer API): This interface provides a high level of detail, offering complete control over the optimization processes. It is perfect for users who require maximum customization of the models.
- Object-Oriented Interface (Fusion API): This API is designed to be more accessible and faster to implement in production environments. The Fusion API allows complex problems to be modeled more intuitively.
- Modeling Languages: Mosek integrates with external modeling languages such as AMPL and Pyomo, making it easier for those familiar with these environments to adopt.
To model an optimization problem using Mosek, we define several key components:
- Variables: These variables represent the values to be optimized, which can be continuous, integer, or binary, defining vectors and matrices within the model.
- Objective Function: It is the mathematical function that we want to maximize or minimize. This function can be linear or quadratic and defines the central objective of the problem, such as maximizing benefits or minimizing costs.
- Constraints: These conditions must be met by the variables, whether linear or nonlinear. Mosek converts these constraints into a matrix format to enhance internal processing and ensure feasible solutions. The search space available after applying all constraints is called the feasible region.
- Model: Encapsulates the variables, the objective function, and the constraints, providing a clear structure for the problem.
- Optimizer: Once the model is ready, the Mosek optimizer is responsible for identifying the best solution that meets all the established criteria.
To illustrate these elements, imagine you have to consume a minimum amount of protein daily but have a limited budget. The dilemma is that some foods you like (such as fish) are very high in protein but expensive, while other foods (such as pasta) are inexpensive but are not a primary source of protein. You want to optimize how much of each food you buy to maximize your protein intake without exceeding your budget while maintaining a balanced diet.

Available optimizers at Mosek
Mosek offers various types of optimizers designed to solve different optimization problems. These optimizers are chosen based on the type of variables (continuous or integer) and the specific nature of the problem. Selecting the appropriate optimizer is essential for obtaining efficient and high-quality solutions.
Problems with continuous variables
A continuous variable can take any value within a specific range. In other words, it is not confined to discrete values. This type of variable is frequently encountered in scenarios that involve representing quantities that can change smoothly, such as distance, time, or temperature.
For problems with continuous variables, Mosek provides two main optimizers: Interior point and Simplex.
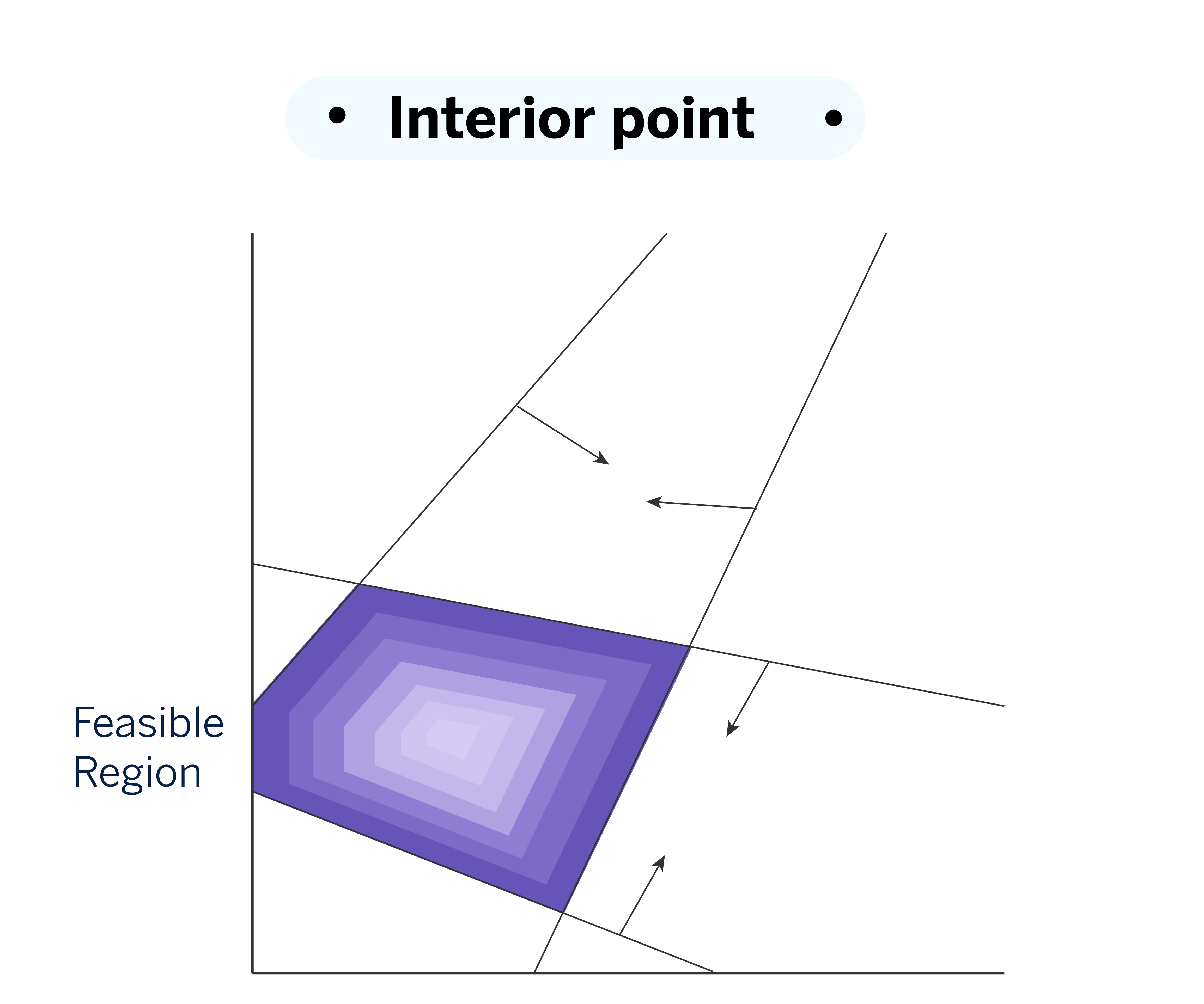
The Interior Point Method stands out as one of the most efficient algorithms for solving large-scale optimization problems, particularly those with numerous constraints and continuous variables. Its strategy involves moving within the feasible region, gradually approaching the edges with each iteration.
To adhere to the internal search strategy, inequality constraints are incorporated into the objective function using a penalty system. As the solution approaches the feasible region boundaries, a penalty is added based on how close the solution is to these boundaries. The penalty decreases gradually, which allows us to explore solutions near the edges in a controlled manner. To find the solution at each step, we solve the equations produced by this new objective function using Newton’s method.
This approach ensures that the algorithm efficiently moves from the interior to the edges of the feasible region, maximizing or minimizing the objective function.

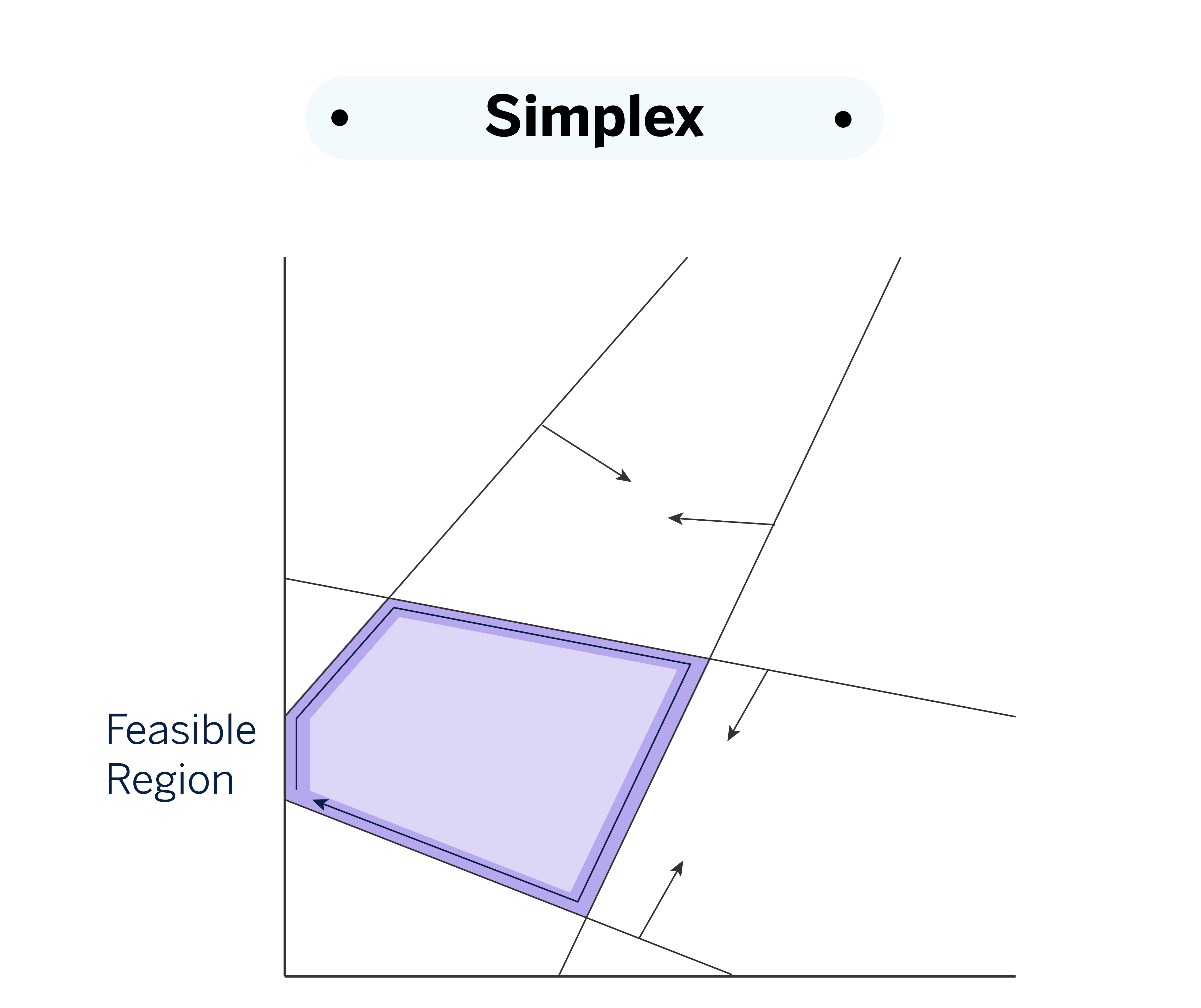
In the Simplex optimizer method, the search is carried out by moving along the vertices of the feasible region. This contrasts with the Interior Point method, which explores the region’s interior instead of its edges. Mosek has three variants for this optimizer: primal_simplex, dual_simplex, and free_simplex.
The primal method directly addresses the initial solution of the problem by adjusting the variables to improve the objective function. In contrast, the dual method solves an associated problem, known as the dual problem, which is derived from the primal problem by using Lagrange multipliers to include the constraints into the optimization process, allowing for a more efficient solution. The free_simplex optimizer automatically selects between the primal and dual versions, choosing the most appropriate strategy according to the characteristics of the problem at hand. This optimizer is especially useful for linear problems.

Problems with integer variables
An integer variable can only hold whole number values without any decimals. These variables are used when quantities cannot be divided into fractions, such as counting the number of people, cars, or any other objects where only discrete values are allowed.
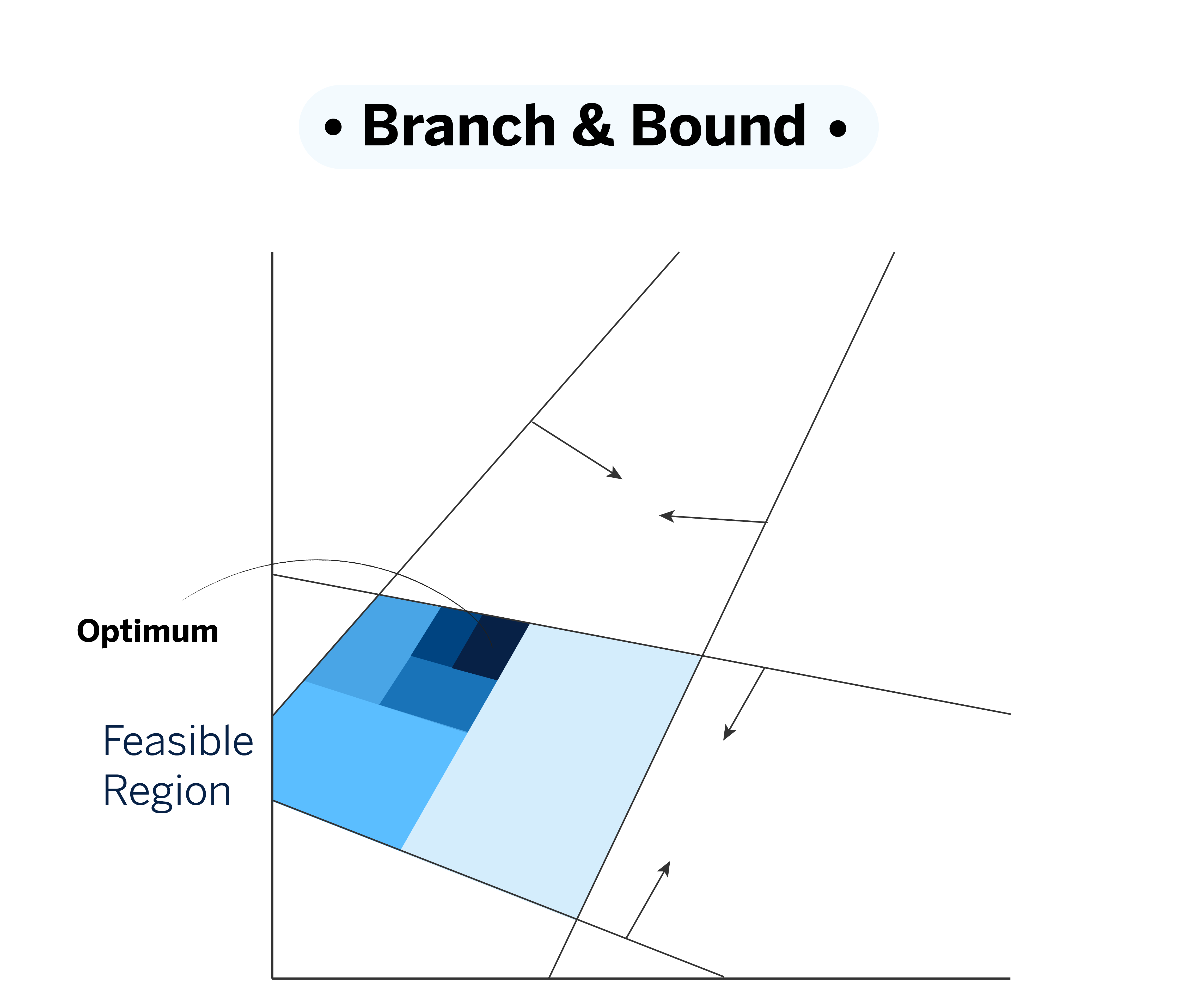
For problems involving integer variables, specialized techniques such as Mixed-Integer Problems (MIP) are used. Mosek has a specific optimizer called “mixed_int,” based on the branch and bound strategy.
Branch and Bound helps in solving optimization problems involving integer variables, such as mixed integer programming (MIP). The concept behind this approach is to break down the original problem into smaller subproblems, known as “branches,” and systematically explore different potential solutions in an organized manner.
The process begins by relaxing the problem, which involves temporarily loosening some constraints to make it easier to find an initial solution. For instance, it may allow a variable that should be binary to temporarily take continuous values, which helps to establish a benchmark. If this solution satisfies the original constraints, it provides a clue as to where the optimal solution might lie.
As the algorithm advances, it eliminates branches that clearly do not improve on the best solution found so far. It focuses only on the options with the most potential, avoiding unnecessary calculations and concentrating resources on the most critical parts of the problem. At each step, the method adjusts the constraints and narrows the search region, refining the solution progressively.

How to determine linearity or non-linearity in an optimization problem
To determine if an optimization problem is linear or nonlinear, it is necessary to analyze both the objective function and the constraints. It is essential to check whether these include higher-order polynomial terms or involve trigonometric, exponential, or logarithmic functions, among others.
The primary distinction between linear and nonlinear problems lies in the nature of their solutions. Linear problems are convex, meaning that any local maximum or minimum is also the global optimum. Nonlinear problems, on the other hand, are more complex because they can have multiple local optima. This implies that we may encounter local solutions that do not necessarily align with the global optimum, thereby making the search for the best possible solution more challenging.
Multiple strategies can be combined to solve mixed integer nonlinear optimization problems. For instance, the branch and bound strategy can be enhanced by incorporating the interior point algorithm and other techniques to solve nonlinear subproblems.