Valores de Shapley y Owen para explicar los resultados de un modelo analítico: un caso práctico

Procedentes de la teoría de juegos cooperativos, estos valores ofrecen un marco sólido para analizar las predicciones realizadas por los modelos analíticos. Nos permiten identificar las contribuciones específicas de cada variable implicada en una determinada predicción, destacando en qué medida influye cada una de ellas en los resultados. Además, revelan las complejas interacciones entre variables, proporcionando una comprensión más profunda de sus efectos combinados.

Utilizando estos valores, podemos lograr una visión más clara de los mecanismos de los modelos de aprendizaje automático, fomentando en última instancia una mayor confianza y comprensión de sus conclusiones.

Este artículo presenta un caso de estudio utilizando el método PartitionExplainer de SHAP, una librería de Python. Con este ejercicio vamos a calcular los valores de Owen para un modelo ensamble de apilamiento de dos niveles en un conjunto de datos público con variables fuertemente correlacionadas. Al incorporar coaliciones de variables, descubrimos que las diferencias entre los valores de Shapley y Owen pueden afectar significativamente a la interpretación del modelo y a la eficiencia computacional, ya que la agrupación de variables reduce el número de combinaciones necesarias para el cálculo.

Hands-on: Descripción del conjunto de datos

Las secciones hands-on de este artículo proporcionan explicaciones paso a paso del ejercicio, incluyendo fragmentos de código Python. Para empezar, importamos las librerías necesarias.

import shap
import numpy as np
import pandas as pd
import seaborn as sns
import scipy.cluster.hierarchy as sch
from scipy.spatial import cKDTree
from scipy.spatial.distance import squareform
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import StackingRegressor

Para este caso de estudio, utilizamos el conjunto de datos públicos California Housing para predecir el valor medio de la vivienda en los distritos de California, expresado en cientos de miles de dólares. Este conjunto de datos de regresión contiene 20.640 registros y 8 columnas.

X, y_ = shap.datasets.california()

Antes de entrar en la fase de modelización, creamos una nueva variable denominada spacial_density utilizando las variables «Latitud» y «Longitud» para capturar la distribución geográfica.

spatial = cKDTree(X[["Latitude", "Longitude"]])
X["spatial_density"] = spatial.query_ball_point(X[["Latitude", "Longitude"]], 0.005, return_length = True)

Posteriormente, eliminamos «Latitud» y «Longitud» para evitar posibles sesgos. Además, la variable objetivo (valor medio de la vivienda) se transformó utilizando una función logarítmica para estabilizar la varianza y mejorar el rendimiento del modelo.

y = pd.DataFrame(np.log(y_), columns=["target"])

xtrain, xtest, ytrain, ytest = train_test_split(
    X.drop(columns=["Latitude","Longitude"]), y,
    test_size=0.1, random_state=42
)

Dadas las relaciones entre determinadas variables, prevemos la formación de coaliciones. Por ejemplo, es probable que «AveBedrms» (número medio de dormitorios) y «AveRooms» (número medio de habitaciones) estén fuertemente correlacionadas, ya que ambas están asociadas con el tamaño medio de las casas de la zona, mientras que «MedInc» (renta mediana) y «Population» son más independientes, ya que las zonas con alta población no tienen necesariamente ingresos medios más altos o más bajos.

## Features correlation

sns.clustermap(
    round(xtrain.corr(),2), method="complete", cmap="RdBu",
    annot=True, annot_kws={"size":9}, vmin=-1, vmax=1, figsize=(8,8)
)

El análisis de correlación muestra que la mayoría de las relaciones entre variables (en valor absoluto) oscilan entre casi cero y 0,85, lo que indica que existen correlaciones entre variables.

Hands-on: Arquitectura del modelo

Utilizamos un modelo ensamble de apilamiento de dos niveles (two-level stacking ensemble model) con dos árboles de decisión como base learners y una regresión lineal como meta learner.

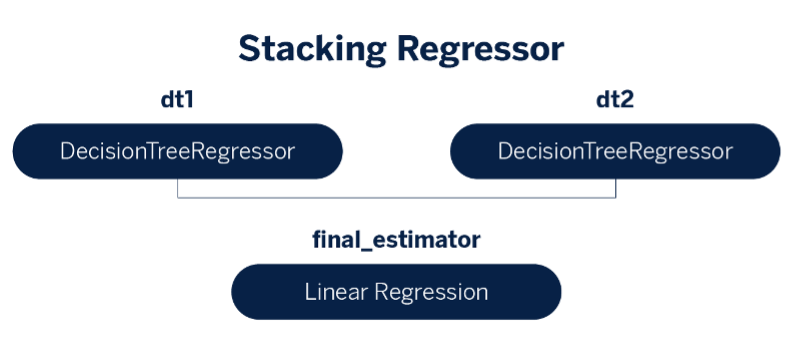
## Model architecture

params_base_learner_1 = {
    "max_depth": 3,
    "random_state": 42
}

params_base_learner_2 = {
    "max_depth": 7,
    "random_state": 42
}

base_learner_1 = DecisionTreeRegressor(**params_base_learner_1)
base_learner_2 = DecisionTreeRegressor(**params_base_learner_2)
meta_learner = LinearRegression()

base_estimators = [("dt1", base_learner_1), ("dt2", base_learner_2)]

model = StackingRegressor(
    estimators=base_estimators,
    final_estimator=meta_learner,
    cv=5,
    n_jobs=-1,
    verbose=5,
)

model.fit(xtrain, np.ravel(ytrain))

El funcionamiento del modelo evaluado con el error cuadrático medio (donde los valores más bajos indican un mejor funcionamiento), muestra una ligera mejora en el conjunto de apilamiento (0,1249) sobre los base learners individuales, con los árboles de decisión puntuando 0,1626 y 0,1259.

Shapley Values: Comprendiendo las contribuciones individuales

Los valores de Shapley son un método de la teoría de juegos cooperativos que nos permite medir la contribución individual de cada variable a la predicción de un modelo.¹ Podemos pensar en la predicción del modelo como una «recompensa» que debe distribuirse equitativamente entre los «jugadores» (las variables). Calculando los valores de Shapley, determinamos la contribución de cada variable a la predicción viendo cómo cambia la predicción cuando añadimos o eliminamos esa variable de varios subconjuntos de variables.

Para calcular los valores de Shapley, utilizamos una función de valor que representa la predicción del modelo basada en cualquier subconjunto de variables. Esta función nos permite medir cuánto cambia la predicción cuando se añade una variable concreta a un subconjunto, capturando la contribución marginal de cada una.²

Debido a que la predicción del modelo depende de todas las variables, incluso de las que no están en el subconjunto en el que nos centramos, utilizamos la marginación para tener en cuenta las variables restantes promediando sus posibles valores. Esto nos permite aislar el impacto específico de las variables de nuestro subconjunto.

El valor Shapley de una variable se calcula promediando sus contribuciones marginales en todos los subconjuntos posibles de variables. De este modo se garantiza que la contribución de cada variable esté representada de forma equitativa. Sin embargo, el cálculo de los valores de Shapley de todos los subconjuntos es muy complejo a medida que aumenta el número de variables, ya que hay que tener en cuenta un número exponencial de subconjuntos.

Para simplificarlo, utilizamos el muestreo de Montecarlo para aproximar los valores de Shapley mediante el muestreo aleatorio de subconjuntos de variables en lugar de evaluarlos todos. Este método consiste en comparar las predicciones del modelo en subconjuntos aleatorios con y sin una variable específica y, a continuación, promediar estas diferencias en muestras de registros para estimar la contribución de la variable.

La desigualdad de Hoeffding: Garantizar la precisión en el muestreo

Al estimar los valores de Shapley mediante muestreo, es importante evaluar lo cerca que están estas aproximaciones de los valores reales. La desigualdad de Hoeffding nos ayuda proporcionando una garantía estadística: limita la probabilidad de que los valores de Shapley basados en el muestreo se desvíen de los valores de Shapley reales en más de una cantidad especificada.

Aplicando la desigualdad de Hoeffding, podemos establecer que, para un número suficientemente grande de muestras K, la probabilidad de que nuestra estimación del valor de Shapley se desvíe del valor real en más de un pequeño margen de error llega a ser muy pequeña. Esto viene dado por:

Esta desigualdad muestra que a medida que aumentamos K, la probabilidad de error significativo disminuye, haciendo que nuestra estimación del valor de Shapley sea más fiable. Por lo tanto, la desigualdad de Hoeffding nos orienta a la hora de elegir un tamaño de muestra adecuado para alcanzar un nivel de precisión aceptable en la estimación del valor de Shapley.

Hands-on: Valores de Shapley para el conjunto de datos California Housing

En nuestro experimento con el conjunto de datos públicos California Housing, utilizamos KernelExplainer de SHAP, que permite apilar modelos de conjunto. KernelExplainer estima los valores de Shapley muestreando subconjuntos y comparando predicciones con y sin cada variable, aplicando los principios anteriores. Aunque KernelExplainer es flexible, asume la independencia de las variables, lo que puede dar lugar a ligeros sesgos cuando las variables están correlacionadas.

## Shapley values through KernelExplainer

K = 2520   # From Hoeffding with p=7, a=-2, b=2, alpha=0.01, epsilon=0.1 

background_data = shap.sample(xtrain, K, random_state=0)
fn = lambda x: model.predict(pd.DataFrame(x, columns=list(xtrain.columns)))

ker_expl = shap.KernelExplainer(fn, background_data, link='identity')
shap_vals_ker = ker_expl(xtest.sample(500, random_state=37))

shap.plots.bar(shap_vals_ker)

Una limitación clave de KernelExplainer es que ignora las dependencias entre variables, incluso cuando están correlacionadas. Esto se debe a que utiliza el muestreo marginal en lugar del condicional. En consecuencia, los valores de Shapley calculados con KernelExplainer pueden estar sesgados por su suposición de que las variables son independientes. Dada la agrupación natural de variables de nuestro experimento, los valores de Owen podrían haber sido una opción más adecuada desde el principio, ya que pueden tener en cuenta las interacciones entre variables.

Valores de Owen: considerando las interacciones entre variables

Al igual que los valores de Shapley, los valores de Owen pretenden distribuir equitativamente la predicción del modelo entre las variables.³ Sin embargo, en lugar de evaluar las variables individualmente, los valores de Owen nos permiten crear coaliciones de variables que actúan conjuntamente.⁴ Por ejemplo, variables como «AveBedrms» y «AveRooms» están muy correlacionadas, por lo que tiene sentido evaluarlas como una coalición en lugar de por separado.

Para calcular los valores de Owen:

1. Primero formamos coaliciones basadas en variables relacionadas.
2. A continuación, tratamos cada coalición como un único «jugador» en el juego cooperativo, calculando el valor de Shapley para cada coalición.
3. Por último, dentro de cada coalición, distribuimos el valor de Shapley de la misma entre las variables individuales en función de sus contribuciones individuales dentro de la coalición.

Este proceso en dos pasos (cálculo de los valores de Shapley para las coaliciones y, a continuación, distribución dentro de cada coalición) garantiza que los valores de Owen reflejen con precisión tanto las contribuciones individuales como las colectivas, especialmente cuando las variables (features) son interdependientes.

Hands-on: Valores de Owen para el conjunto de datos California Housing

Para calcular los valores de Owen en la práctica, podemos utilizar PartitionExplainer de SHAP, que nos permite especificar coaliciones de variables basadas en sus interacciones. Al agrupar variables correlacionadas en grupos, podemos crear coaliciones que reflejen mejor las dependencias del mundo real, capturando su influencia colectiva.

## Correlation-based clusters of features
dist = 1 - np.abs(xtrain.corr())   # distance matrix
condensed = squareform(dist)
clust = sch.linkage(condensed, method="complete")

# Equivalently, we can use the following one-line code
# clust = shap.utils.hclust(xtrain, metric="correlation")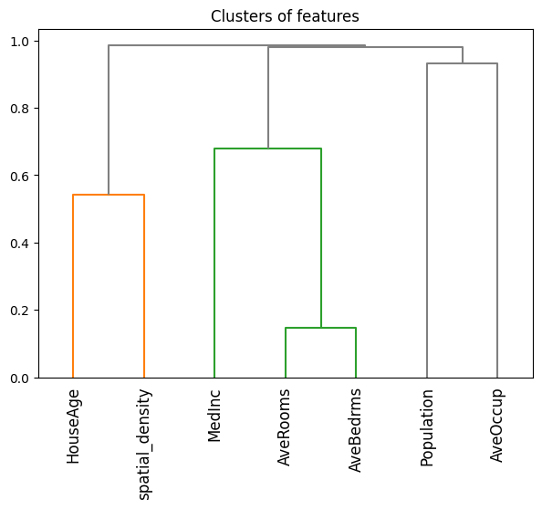

A continuación, especificamos estos grupos de variables para el PartitionExplainer a través del parámetro clustering, como se muestra a continuación.

## Shapley values through PartitionExplainer

masker = shap.maskers.Partition(xtrain, clustering=clust)

part_expl = shap.PartitionExplainer(fn, masker)
shap_vals_part = part_expl(xtest.sample(500, random_state=37))

shap.plots.bar(shap_vals_part, clustering_cutoff=0.75)

Conclusiones

A la hora de aplicar explicabilidad al aprendizaje automático, elegir entre los valores de Shapley o los valores de Owen es una decisión estratégica. Los valores de Shapley destacan en el análisis de contribuciones independientes, mientras que los valores de Owen son más adecuados para captar interacciones dentro de grupos de variables. Esta distinción es crucial cuando existen dependencias, ya que los valores de Owen reflejan mejor las influencias conjuntas.

Cuando las variables están correlacionadas, el uso de KernelExplainer de la biblioteca SHAP puede dar lugar a resultados sesgados, ya que este método asume que todas las variables son independientes. En los casos en los que las variables forman grupos de forma natural, los valores de Owen ofrecen una alternativa mejor al capturar con precisión las interacciones de las variables a través de coaliciones agrupadas.

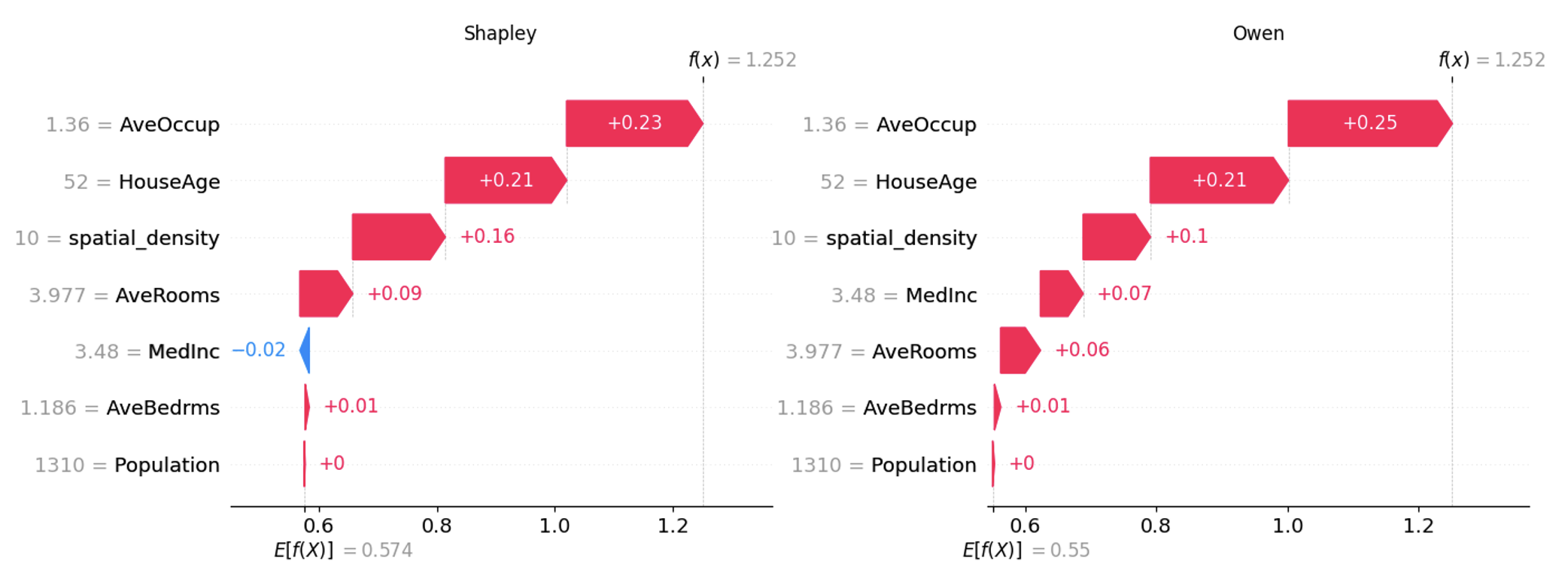
La combinación de los valores de Shapley y los valores de Owen resulta beneficiosa en modelos complejos con variables independientes e interdependientes. Esta estrategia híbrida mejora la transparencia y la confianza en el modelo, al tiempo que permite a los científicos de datos ofrecer explicaciones que se ajustan a la estructura de los datos, lo que permite una toma de decisiones más informada y fiable.