
En búsqueda de la solución definitiva: optimización matemática con Mosek
Un mismo problema puede tener múltiples soluciones, pero surge la pregunta: ¿cuál es la más adecuada? Desde una perspectiva cuantitativa, lo “óptimo” es aquello que supera todas las demás alternativas.
Sin embargo, lo que es mejor dependerá del contexto (variables) y de las opciones disponibles, lo que complejiza la toma de decisiones. Para abordar estos problemas, existen herramientas matemáticas que nos permiten crear un marco concreto y medible del alcance de un problema. Así, podemos tomar decisiones basadas en datos, lo que reduce la incertidumbre, además de asegurar que nuestras elecciones están bien fundamentadas.
En el ámbito de las matemáticas y la ingeniería, la optimización busca maximizar o minimizar una función conocida como función objetivo. Esta describe un determinado fenómeno o proceso, ayudando a mejorar la eficiencia, reducir costos o aumentar el rendimiento, según las necesidades del problema planteado.
Un problema de optimización consiste en determinar el valor de una o más variables que maximizan o minimizan la función objetivo, denotada como f(x), la cual depende de un conjunto de variables (x). Durante este proceso, las variables no son completamente libres; están sujetas a restricciones que limitan los valores que pueden tomar. Estas pueden ser restricciones de igualdad o de desigualdad.
Problemas de optimización: tipos de restricciones
Las restricciones de desigualdad, representadas como g(x) ≤ 0, limitan las variables para que no superen ciertos valores o límites. Por ejemplo, en un problema de producción, podría significar que la cantidad producida no puede exceder la capacidad de la fábrica.
Por otro lado, las restricciones de igualdad, representadas como h(x)=0, exigen que las variables cumplan una condición exacta. Por ejemplo, en un presupuesto, la suma de gastos debe ser igual a los ingresos disponibles. El objetivo es encontrar el conjunto de valores de (x) que optimice la función f(x), respetando tanto las desigualdades como las igualdades, garantizando que la solución es factible y óptima.
Eligiendo un optimizador: comparativa de competidores y benchmarking
En el mercado de la optimización matemática, herramientas como Gurobi, CPLEX, Xpress, Mosek y SCIP son ampliamente reconocidas por resolver problemas complejos, cada una con fortalezas específicas. Gurobi destaca por su velocidad en problemas con restricciones enteras (MIP), aunque a veces sacrifica la calidad de las soluciones.
CPLEX es robusto en problemas lineales y a gran escala, pero puede enfrentar dificultades con estructuras más complejas o no lineales. Xpress y SCIP son opciones populares en ámbitos académicos, siendo Xpress fuerte en problemas lineales y no lineales, mientras que SCIP es valorado por su flexibilidad en optimización combinatoria.
Mosek, por su parte, se presenta como una herramienta especialmente eficaz para resolver problemas de optimización que incluyen múltiples restricciones complejas y modelos de gran escala. Aunque su tiempo de ejecución por nodo (es decir, el tiempo que tarda en analizar cada posible solución dentro del problema) es más lento que el de Gurobi, esta aparente desventaja es compensada por su capacidad para centrarse en las regiones más prometedoras del espacio de búsqueda, es decir, aquellas áreas donde es más probable encontrar soluciones de alta calidad.
Este enfoque permite a Mosek evitar gastar recursos en explorar soluciones que probablemente no sean útiles, lo que hace que el proceso sea más eficiente a largo plazo. Esta cualidad lo convierte en una herramienta confiable para aplicaciones que requieren un balance delicado entre precisión y eficiencia, especialmente en contextos donde la calidad de la solución no puede ser comprometida. Tras comparar estas características con las de otros optimizadores, optamos por Mosek.
Conociendo Mosek
Mosek es un software de optimización matemática diseñado para resolver una amplia variedad de problemas, incluidos los lineales, no lineales, cuadráticos y cónicos. Su principal fortaleza radica en la capacidad de manejar problemas grandes y complejos de manera eficiente. Además, proporciona herramientas avanzadas para utilizar tanto restricciones de desigualdad como de igualdad.
Existen tres vías o interfaces para hacer uso de esta herramienta:
- Interfaz Orientada a Matrices (Optimizer API): Esta interfaz permite trabajar a un nivel muy detallado, proporcionando un control total sobre los procesos de optimización. Es ideal para usuarios que necesitan personalizar los modelos al máximo.
- Interfaz Orientada a Objetos (Fusion API): Esta API está diseñada para ser más accesible y rápida de implementar en entornos de producción. Fusion API permite modelar problemas complejos de una manera más intuitiva. Es en la que nos centraremos.
- Lenguajes de Modelado: Mosek también se integra con lenguajes de modelado externos como AMPL y Pyomo, lo que facilita su adopción por aquellos que ya están familiarizados con estos entornos.
Para modelar un problema de optimización con Mosek, se definen varios componentes clave:
- Variables: Éstas son los valores a determinar mediante la optimización, y pueden ser continuas, enteras o binarias. Estas variables definen tanto vectores como matrices dentro del modelo.
- Función Objetivo: Es la función matemática que queremos maximizar o minimizar, y puede ser lineal o cuadrática. Esta función define el objetivo central del problema, como maximizar beneficios o minimizar costos.
- Restricciones: Estas son las condiciones que las variables deben cumplir, ya sean lineales o no lineales. Mosek convierte estas restricciones en un formato de matriz para mejorar su procesamiento interno y garantizar que las soluciones sean viables. El espacio de búsqueda disponible tras aplicar todas las restricciones se denomina región factible.
- Modelo: Encapsula las variables, la función objetivo y las restricciones, proporcionando una estructura clara para el problema.
- Optimizador: Una vez construido el modelo, el optimizador de Mosek se encarga de encontrar la mejor solución posible, cumpliendo con todos los criterios establecidos.
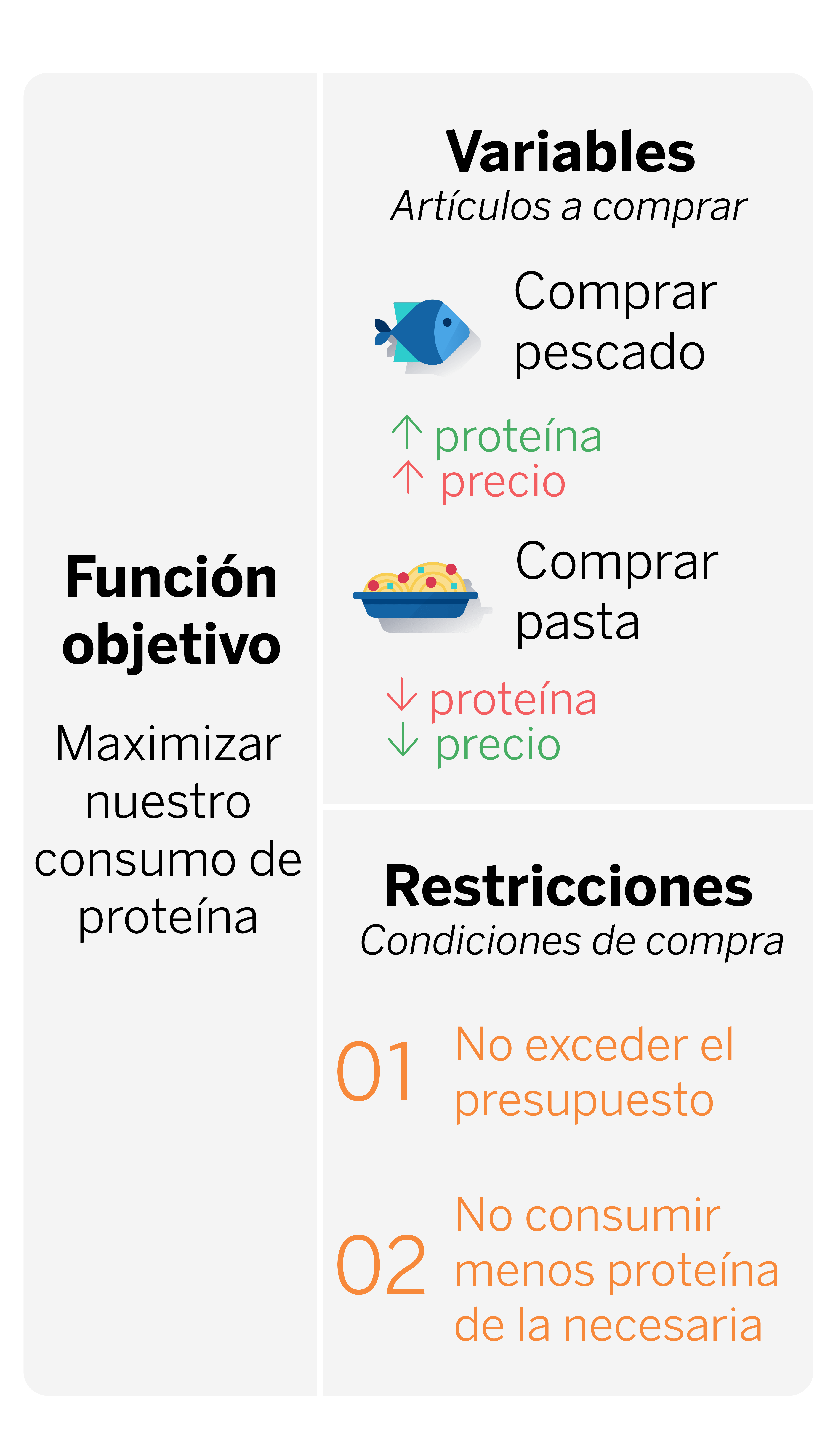
Para ilustrar estos elementos, imagina que tienes que consumir una cantidad mínima de proteínas al día, pero tienes un presupuesto limitado. El dilema es que algunos alimentos que te gustan (como el pescado) son muy ricos en proteínas pero costosos, mientras que otros alimentos (como la pasta) son baratos pero no son una fuente primaria de proteínas. Quieres optimizar cuánto comprar de cada alimento para maximizar tu ingesta de proteína sin exceder tu presupuesto, manteniendo una dieta balanceada.
Optimizadores disponibles en Mosek
Mosek cuenta con varios tipos de optimizadores diseñados para resolver diferentes clases de problemas de optimización. Estos optimizadores se seleccionan en función de la naturaleza de las variables (continuas o enteras) y el tipo de problema que se desea resolver. La elección del optimizador adecuado es crucial para obtener soluciones eficientes y de alta calidad.
Problemas con variables continuas
Una variable continua puede tomar cualquier valor dentro de un rango específicos decir, no está limitada a valores discretos. Este tipo de variable es común en problemas que modelan cantidades que pueden ser fraccionadas, como la distancia, el tiempo o la temperatura.
Para problemas donde las variables son continuas, Mosek ofrece dos optimizadores principales: Punto interior y Simplex.
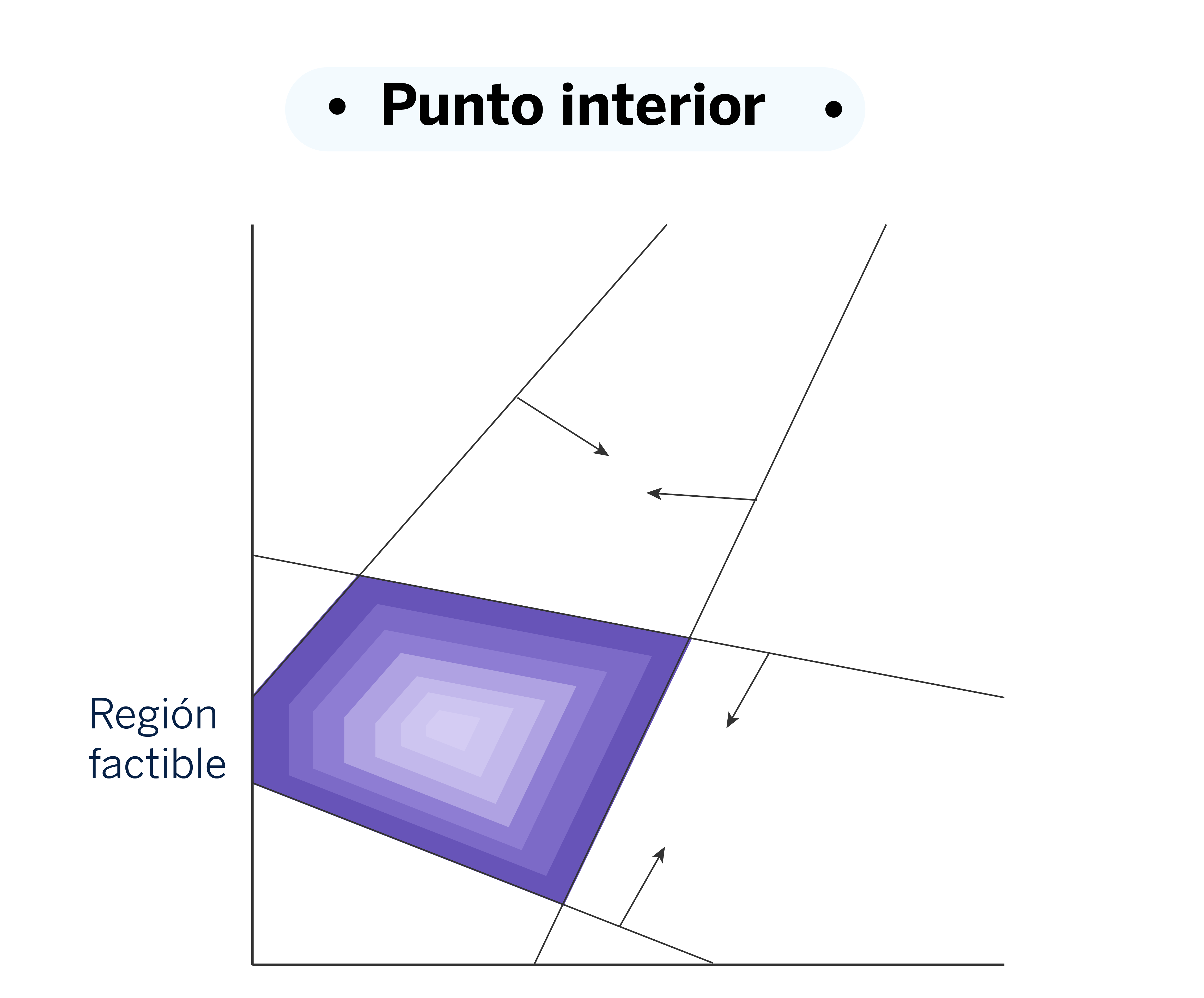
El método de Punto Interior (Interior Point Method) es uno de los algoritmos más eficaces para resolver problemas de optimización a gran escala, especialmente aquellos con muchas restricciones y variables continuas. Su estrategia se basa en moverse dentro de la región factible, acercándose progresivamente a los bordes en cada iteración.
Para cumplir con esta estrategia de búsqueda interna, las restricciones de desigualdad se integran en la función objetivo mediante un sistema de penalizaciones. A medida que la solución se acerca a los límites de la región factible, se añade una penalización cuyo valor depende de la proximidad a dichos límites. El peso de esta penalización disminuye progresivamente, lo que permite explorar soluciones más cercanas a los bordes de manera controlada. Para obtener la solución en cada paso, se resuelven las ecuaciones generadas por esta nueva función objetivo utilizando el método de Newton.
Este enfoque garantiza que el algoritmo se mueva desde el interior hacia los bordes de la región factible, maximizando o minimizando la función objetivo de manera eficiente.

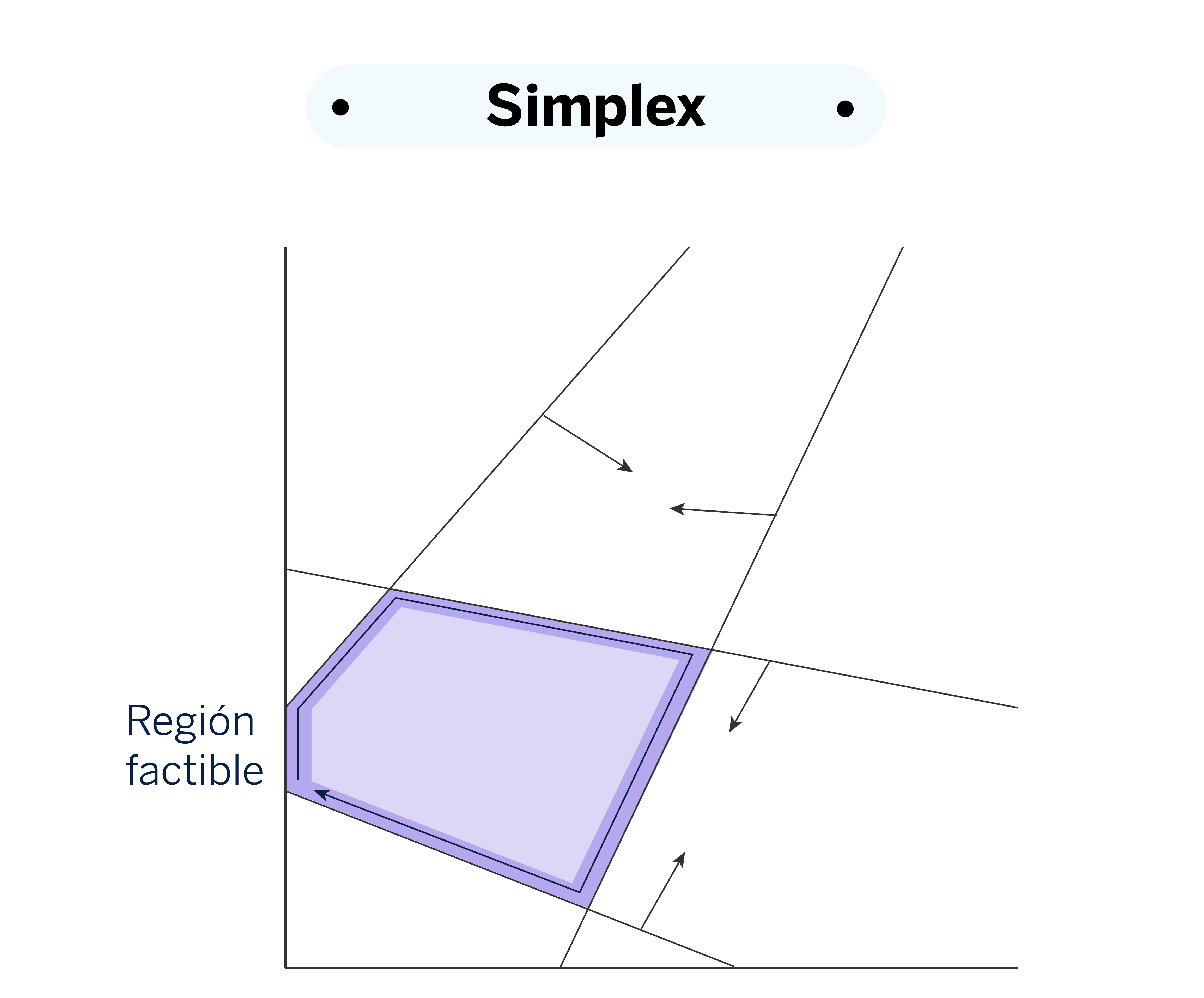
En el método Simplex, la búsqueda se lleva a cabo moviéndose a lo largo de los vértices de la región factible. Esto contrasta con el método de Punto interior, que explora el interior de la región en lugar de sus bordes. Mosek posee tres variantes para este optimizador: primal_simplex, dual_simplex, y free_simplex.
El método primal aborda directamente la solución inicial del problema, ajustando las variables para mejorar la función objetivo. En cambio, el método dual resuelve un problema asociado, conocido como el problema dual, que se deriva del problema primal utilizando multiplicadores de Lagrange para integrar las restricciones en el proceso de optimización, lo que permite una resolución más eficiente. El optimizador free_simplex selecciona automáticamente entre las versiones primal y dual, eligiendo la estrategia más adecuada según las características del problema específico. Este optimizador es especialmente útil para problemas lineales.

Problemas con variables enteras
Una variable entera solo puede tomar valores enteros, es decir, números sin decimales. Estas variables se presentan en situaciones donde las cantidades no pueden dividirse en fracciones, como el número de personas, coches, o cualquier conteo donde solo se admiten valores discretos.
Para problemas que incluyen variables enteras, se utilizan técnicas especiales como los Mixed-Integer Problems (MIP). Mosek posee un optimizador específico denominado “mixed_int” basado en la estrategia de branch and bound.
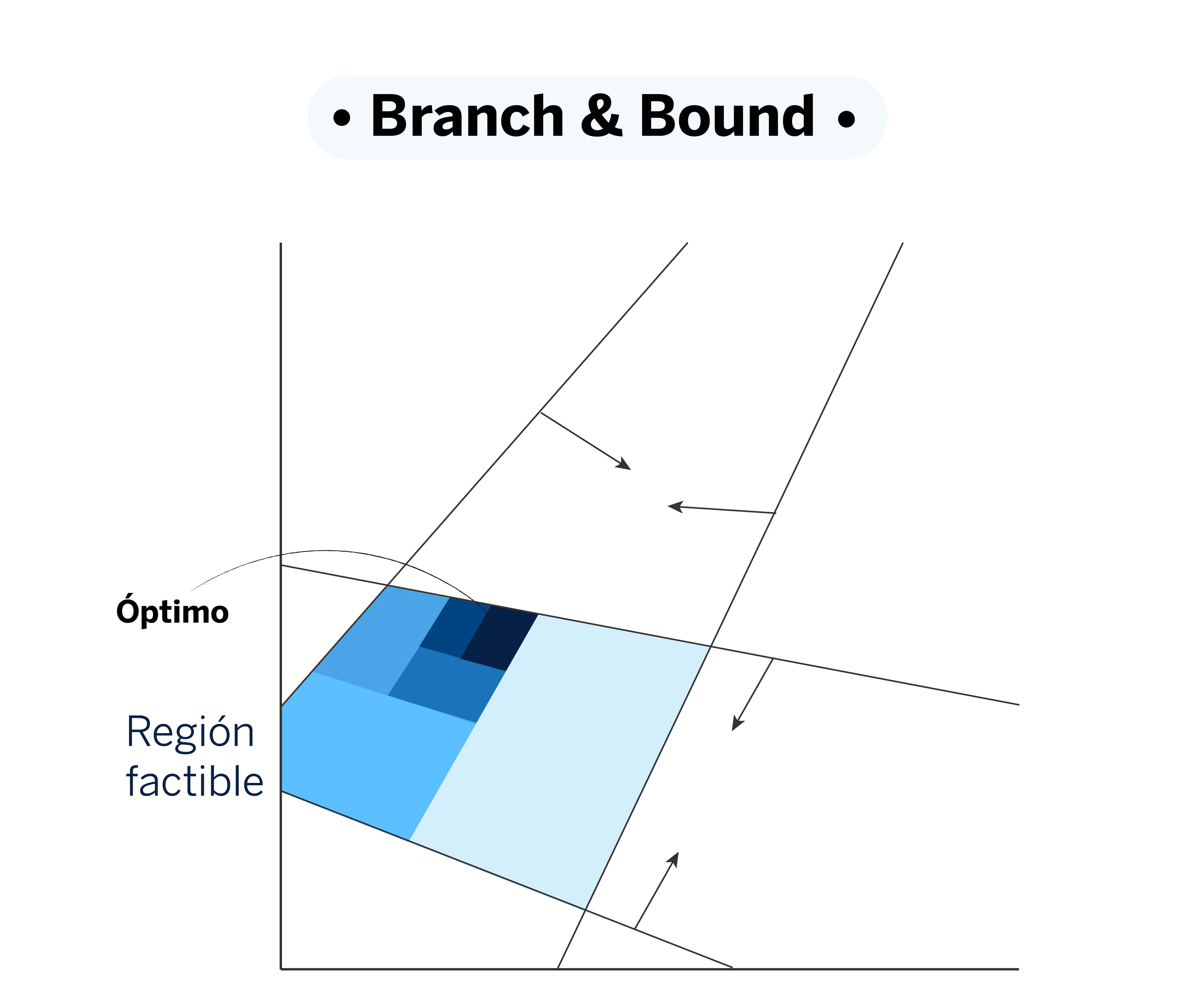
Branch and Bound es una técnica para resolver problemas de optimización que incluyen variables enteras, como los conocidos Mixed-Integer Programming (MIP). La idea detrás de este método es dividir el problema original en subproblemas más pequeños, llamados “ramificaciones”, explorando diferentes posibles soluciones de manera ordenada y sistemática.
El proceso arranca relajando el problema; es decir, suavizando temporalmente algunas restricciones para hacer más sencilla la obtención de una solución inicial. Por ejemplo, permite que una variable que debería ser binaria tome valores continuos temporalmente, lo que ayuda a establecer una cota de referencia. Si esta solución cumple con las restricciones originales, ya tenemos una pista de por dónde va la solución óptima.
A medida que el algoritmo avanza, va descartando ramificaciones que claramente no mejoran la mejor solución encontrada hasta el momento, y se enfoca solo en las opciones con más potencial. Esto evita cálculos innecesarios y concentra los recursos en las partes del problema que realmente importan. En cada paso, el método ajusta las restricciones y reduce la región de búsqueda, afinando cada vez más la solución.

Linealidad y no linealidad
Para determinar si un problema de optimización es lineal o no lineal, es necesario analizar tanto la función objetivo como las restricciones. Debemos comprobar si estas incluyen términos polinómicos de orden superior, o si utilizan funciones trigonométricas, exponenciales o logarítmicas, entre otras.
La principal diferencia entre los problemas lineales y no lineales radica en la naturaleza de sus soluciones. Los problemas lineales son convexos, lo que implica que cualquier máximo o mínimo local es también el óptimo global. Por otro lado, los problemas no lineales son más complejos, ya que es posible que tengan múltiples óptimos locales. Esto significa que podríamos encontrar soluciones locales que no necesariamente coinciden con el óptimo global, lo cual complica el proceso de búsqueda de la mejor solución posible.
En problemas no lineales (“mixed integer non linear optimization”) pueden combinarse varias estrategias en la resolución de un mismo problema. Por ejemplo, dentro de la estrategia de branch and bound, es posible utilizar el algoritmo de punto interior junto con otras técnicas para resolver los subproblemas no lineales.