Estrategias para abordar problemas de clasificación: nuestro primer Quick Study

La creación de modelos de inteligencia artificial comprende varias fases, entre las cuales suelen destacarse las fases de entrenamiento y de evaluación. Para garantizar el correcto desempeño de los modelos, los científicos de datos deben realizar una compleja labor de selección de métricas para evaluarlos una vez han sido entrenados. La complejidad radica en que algunas métricas serán más adecuadas que otras en función del caso de uso.

Las métricas de evaluación poseen ventajas y desventajas que deben ser valoradas antes de su implementación, por lo que no existe un consenso sobre si existe una métrica mejor que las demás para evaluar modelos. En este sentido, las métricas suelen elegirse ad hoc al caso de uso, lo que implica que, dado que las problemáticas se abordan individualmente, éstas requieren una exhaustiva labor de cálculo con diferentes métricas y, en consecuencia, una gran inversión de tiempo y esfuerzo.

Desde BBVA AI Factory quisimos establecer una estrategia común que nos permitiese tener una guía de uso de métricas, de manera que cada vez que nos enfrentemos a la evaluación de un modelo podamos discernir cuál es la más adecuada. Esta propuesta surge en el marco de problemas de clasificación, específicamente sobre modelos de clasificación multiclass y multilabel. Para llevarla a cabo, realizamos un quick study, una de las iniciativas de exploración e innovación con datos que hemos establecido en AI Factory.

Motivación del Quick Study: los problemas multiclass y multilabel

Un quick study, como su propio nombre indica, es un estudio teórico sobre una problemática concreta que se realiza en un corto período de tiempo. Estos estudios buscan llegar a conclusiones que sean útiles para varios equipos; es decir, poseen cierto grado de transversalidad, y resultan en la compartición de conocimiento para establecer estrategias comunes de actuación. Dichas estrategias consideran el estado del arte en técnicas innovadoras que pueden extrapolarse a diferentes casos de uso.

El objetivo del primer Quick Study realizado en BBVA AI Factory es proporcionar una respuesta al problema de evaluación de modelos multiclase (multiclass) y/o multietiqueta (multilabel). Varios equipos en nuestro hub trabajan con problemas de clasificación, por lo que se puso de manifiesto la necesidad de comparar las diferentes técnicas de evaluación y sentar las bases de una propuesta transversal.

Los problemas multiclase son aquellos en los que tenemos varias etiquetas disponibles para cada muestra, pero, finalmente, a cada observación o sample sólo se le asocia una única etiqueta sobre la cual se realiza una única predicción. Un ejemplo para explicarlo: vemos la imagen de un perro junto a una planta, y tenemos las etiquetas “perro”, “gato”, “bus” y “planta”. El modelo sólo identificará uno de los elementos como verdadero, a pesar de que en la realidad ambos elementos están en la imagen. Este tipo de modelos únicamente asocian la etiqueta que han aprendido como la más probable: en este caso, el perro.

Por otro lado, los problemas multilabel admiten más de una etiqueta para cada muestra. En este caso, retomando el ejemplo anterior, el modelo puede tener aciertos parciales, como puede serlo identificar tanto al perro como a la planta. Esto quiere decir que puede asignar algunas de las etiquetas, o todas, o ninguna, en función de la calidad del modelo y del problema de clasificación que se le presente.

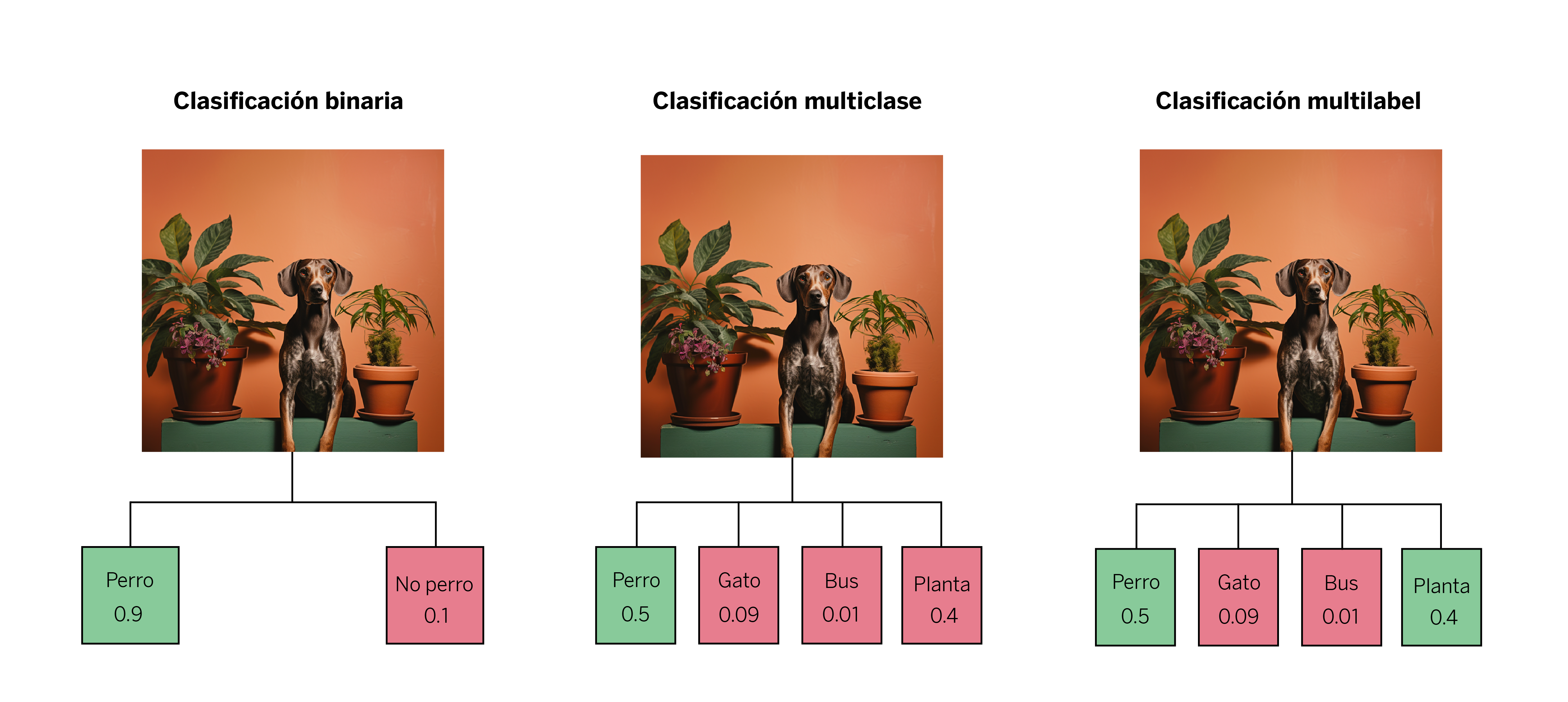
Uno de los casos de uso que motivó este quick study es el problema de clasificación que surge en las conversaciones entre clientes y gestores de BBVA a través de la app del banco. Cuando queremos determinar de qué producto se está hablando, existe un problema multilabel, pues a la misma conversación se le pueden asignar diferentes productos y, por ende, diferentes etiquetas.

Contamos con una taxonomía -o grupos de temáticas- de 14 posibles productos que pueden asociarse a las conversaciones. Para entrenar nuestro modelo tenemos una muestra de conversaciones etiquetadas, pero hay un problema: la distribución de los productos no es equitativa, ya que, por ejemplo, el volumen de conversaciones sobre “cuentas” y “tarjetas” (productos dentro de la taxonomía) no es igual que el volumen de conversaciones sobre “nóminas” o “avales” (menos habituales).

Para intentar resolver este problema, se probaron distintas estrategias de modelado:

1. Utilizar la muestra etiquetada sin balancear, lo que empeoró los resultados respecto a los productos minoritarios.
2. Tratar de balancear el volumen de todos los productos, obteniendo esta vez peores resultados respecto a los productos mayoritarios.
3. Tratar de buscar un equilibrio entre la cantidad de productos mayoritarios y minoritarios. Esta estrategia no arrojaba los mejores resultados ni para los productos mayoritarios ni para los minoritarios.

Ante la dificultad de elegir una estrategia de modelado u otra, pusimos el foco en las métricas. Cada una de las estrategias anteriores presenta una serie de métricas (a nivel individual para cada producto y a nivel global sobre el modelo) que van mejorando o empeorando en función de en qué nos vamos fijando. Teniendo esto en cuenta, finalmente nos preguntamos: ¿Con qué métricas de todas las probadas nos quedamos?

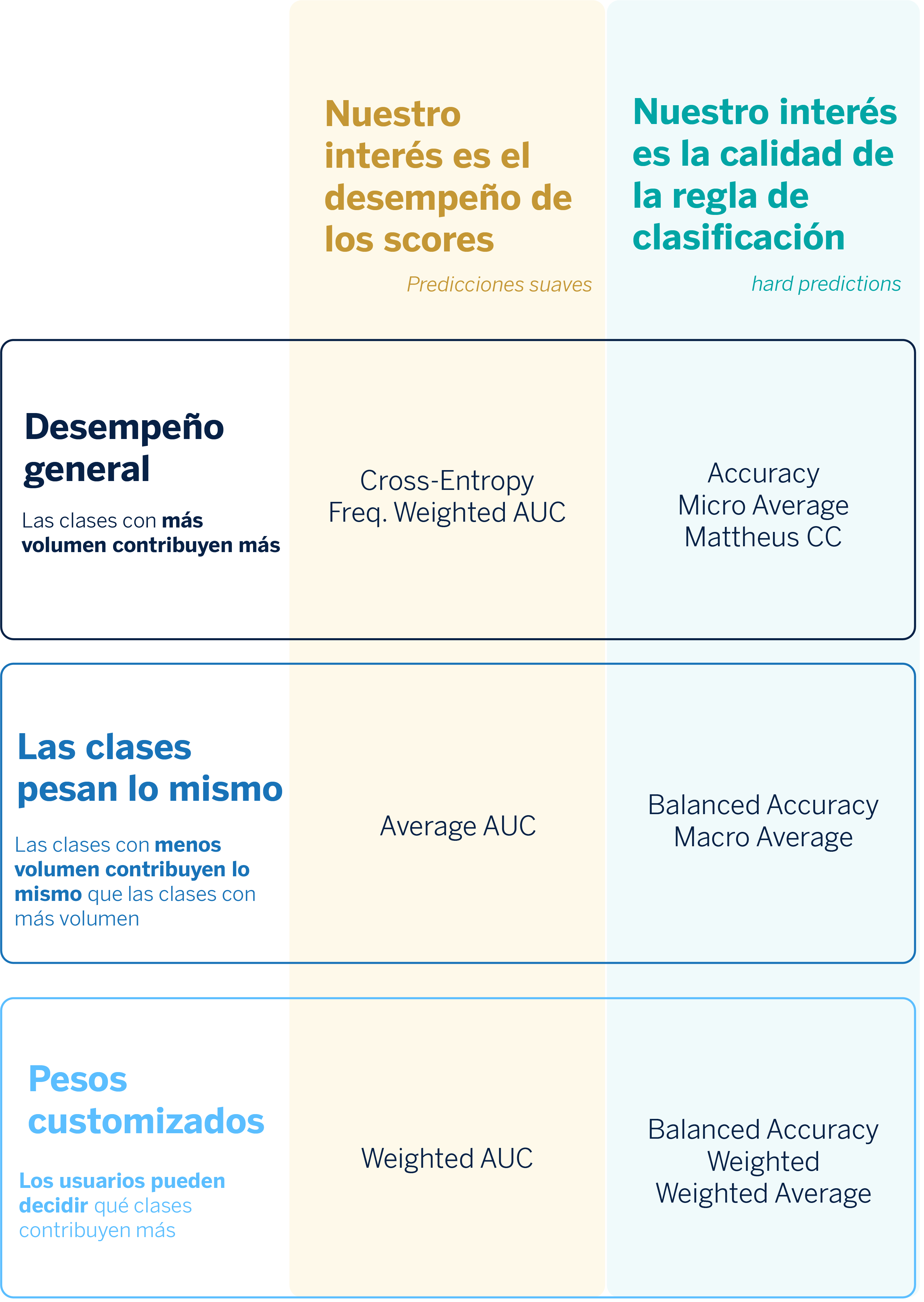
Comprendiendo las ventajas y desventajas de cada métrica en los problemas multiclase¹

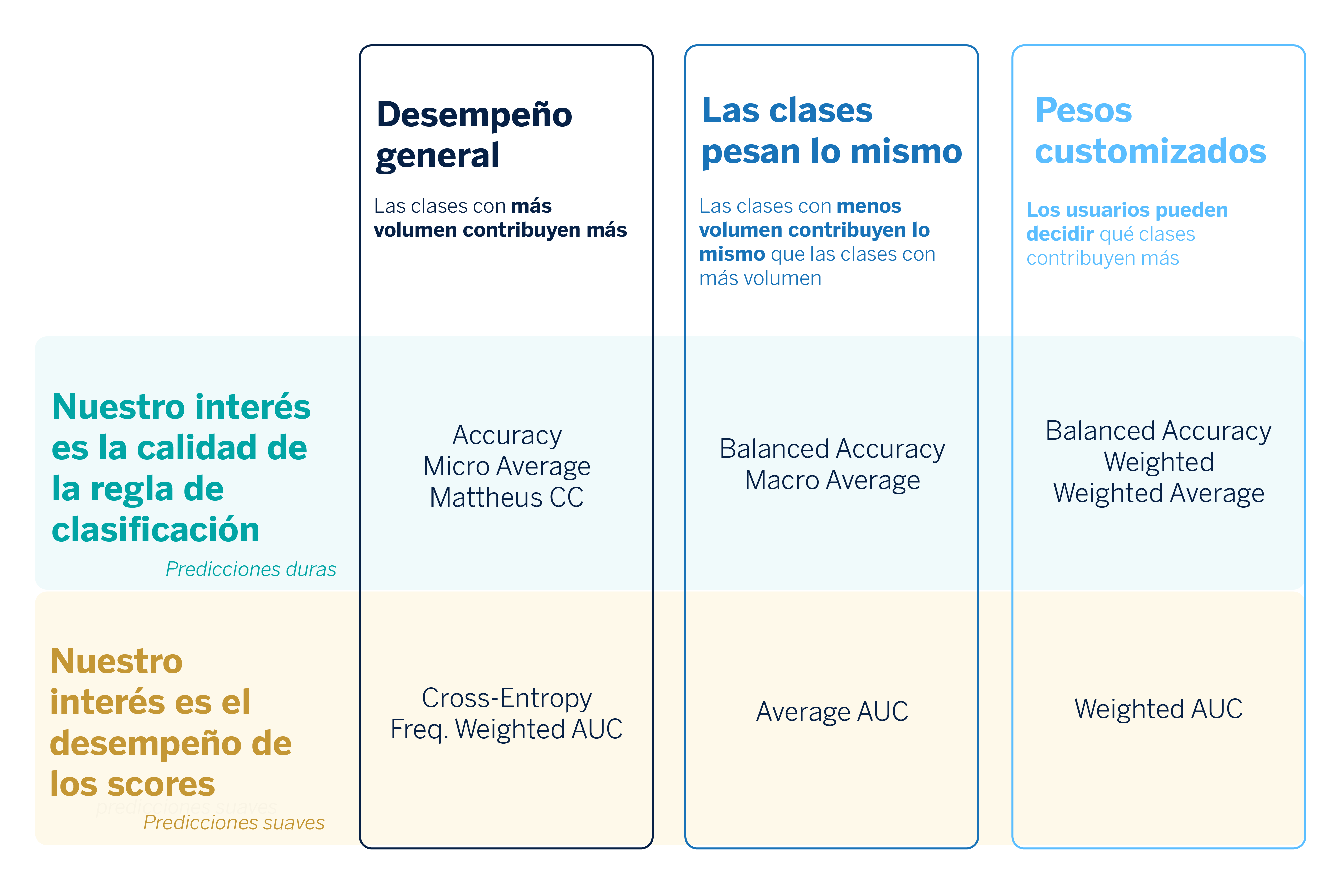
En el contexto de problemas de clasificación (tanto binaria, como multiclase y multietiqueta), debemos distinguir entre las predicciones duras y las predicciones suaves. La predicción suave se refiere a la probabilidad estimada de que una observación pertenezca a una de las clases, mientras que la predicción dura se refiere directamente a la clase que predice el modelo para una observación. Además, hay que tener en cuenta que en los problemas multiclase se asigna una única etiqueta a cada obeservación, aunque puedan darse varias etiquetas en la realidad. Con todo, contamos con dos tipologías de métricas que dependen de lo que quiera evaluarse.

• Calidad de las predicciones duras (hard predictions)
• Calidad de los scores o predicciones suaves (soft predictions)

Partimos de la idea de que no hay métrica mala, sino que sus ventajas y desventajas dependen del objetivo al que queremos llegar en un caso de uso.

Calidad de las predicciones duras (hard predictions)

A continuación, nos adentramos en cada una de las métricas que nos ayudan a determinar la calidad de las predicciones duras, para así conocer su función, fórmula, ventajas y desventajas.

Accuracy

Indica cuántas observaciones son clasificadas correctamente sobre el número de observaciones totales.

Ventajas	Desventajas
Adecuada en el caso que nuestro objetivo sea clasificar correctamente el mayor número de muestras posible.	Las clases más representadas en nuestro dataset tendrán más peso en la métrica, por lo que no nos será útil por ejemplo para garantizar un buen comportamiento en las clases minoritarias.

Balanced Accuracy

Mide la precisión de cada clase individualmente y luego las promedia dividiendo entre el número de clases.

Ventajas	Desventajas
Útil cuando se quiere que el modelo se comporte igual de bien en todas las clases, ya que todas tienen el mismo peso, por lo que ayuda a mejorar el comportamiento en las clases menos representadas.	Puede ser poco conveniente esta métrica si lo que nos interesa es tener una buena predicción en el dataset como conjunto.

Balanced Accuracy Weighted

Mide la precisión de cada clase y luego promedia utilizando unos pesos específicos.

Ventajas	Desventajas
Se le asigna a cada clase un peso específico, por lo que se puede adaptar a las necesidades de cada caso de uso.	Muchas veces, en problemas reales, es difícil determinar el peso de cada clase, pudiendo no reflejar bien la realidad.

Micro Average (precision, recall, f1)

Se consideran todas las observaciones de manera conjunta, por lo que se miden aciertos en general, independientemente de la clase.

Ventajas	Desventajas
Posee las mismas ventajas que la Accuracy.	Posee las mismas desventajas que la Accuracy.

Macro Average (precision, recall, f1)

Se considera la media de métricas (precision, recall, f1) en cada clase individual.

Ventajas	Desventajas
Posee las mismas ventajas que la Balanced Accuracy.	Posee las mismas desventajas que la Balanced Accuracy.

Weighted Average (precision, recall, f1)

Parte de las fórmulas Macro Average multiplicando cada precisión o recall por el peso personalizado de cada clase.

Ventajas	Desventajas
Posee las mismas ventajas que la Balanced Accuracy Weighted.	Posee las mismas desventajas que la Balanced Accuracy Weighted.

Mattheus Correlation Coefficient

Su fórmula está basada en la relación entre los elementos correcta y erróneamente clasificados.

Ventajas	Desventajas
Más robusta frente a problemas con desbalanceo de clases.	Poco interpretable. Aunque se suaviza la contribución de las clases más representadas, estas siguen teniendo más peso.

Cohen’s Kappa

Medida de la proximidad entre las clases predichas y las clases reales donde se compara el modelo con una clasificación aleatoria acorde a la distribución de cada clase.

Ventajas	Desventajas
Puede corregir sesgos de la precisión general cuando trata con datos desbalanceados.	Poco interpretable. Cuanto más diste la distribución con la que se está entrenando de la distribución real menos podremos comparar estas métricas entre sí; por ello, no se pueden probar diferentes estrategias de desbalanceo.

Accuracy

Indica cuántas observaciones son clasificadas correctamente sobre el número de observaciones totales.

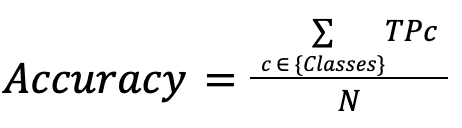
Ventajas
Adecuada en el caso que nuestro objetivo sea clasificar correctamente el mayor número de muestras posible.

Desventajas
Las clases más representadas en nuestro dataset tendrán más peso en la métrica, por lo que no nos será útil por ejemplo para garantizar un buen comportamiento en las clases minoritarias.

---

Balanced Accuracy

Mide la precisión de cada clase individualmente y luego las promedia dividiendo entre el número de clases.

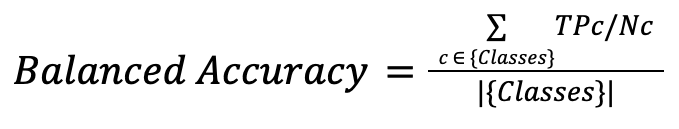
Ventajas
Útil cuando se quiere que el modelo se comporte igual de bien en todas las clases, ya que todas tienen el mismo peso, por lo que ayuda a mejorar el comportamiento en las clases menos representadas.

Desventajas
Puede ser poco conveniente esta métrica si lo que nos interesa es tener una buena predicción en el dataset como conjunto.

---

Balanced Accuracy Weighted

Mide la precisión de cada clase y luego promedia utilizando unos pesos específicos.

Ventajas
Se le asigna a cada clase un peso específico, por lo que se puede adaptar a las necesidades de cada caso de uso.

Desventajas
Muchas veces, en problemas reales, es difícil determinar el peso de cada clase, pudiendo no reflejar bien la realidad.

---

Micro Average (precision, recall, f1)

Se consideran todas las observaciones de manera conjunta, por lo que se miden aciertos en general, independientemente de la clase.

Ventajas
Posee las mismas ventajas que la Accuracy.

Desventajas
Posee las mismas desventajas que la Accuracy.

---

Macro Average (precision, recall, f1)

Se considera la media de métricas (precision, recall, f1) en cada clase individual.

Ventajas
Posee las mismas ventajas que la Balanced Accuracy.

Desventajas
Posee las mismas desventajas que la Balanced Accuracy.

---

Weighted Average (precision, recall, f1)

Parte de las fórmulas Macro Average multiplicando cada precisión o recall por el peso personalizado de cada clase.

Ventajas
Posee las mismas ventajas que la Balanced Accuracy Weighted.

Desventajas
Posee las mismas desventajas que la Balanced Accuracy Weighted.

---

Mattheus Correlation Coefficient

Su fórmula está basada en la relación entre los elementos correcta y erróneamente clasificados.

Ventajas
Más robusta frente a problemas con desbalanceo de clases.

Desventajas
Poco interpretable. Aunque se suaviza la contribución de las clases más representadas, estas siguen teniendo más peso.

---

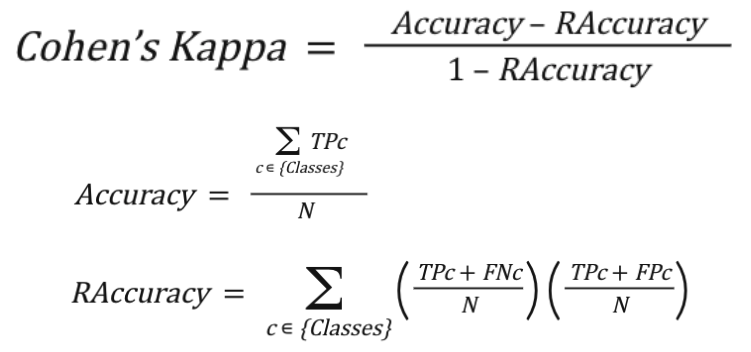
Cohen’s Kappa

Medida de la proximidad entre las clases predichas y las clases reales donde se compara el modelo con una clasificación aleatoria acorde a la distribución de cada clase.

Ventajas
Puede corregir sesgos de la precisión general cuando trata con datos desbalanceados.

Desventajas
Poco interpretable. Cuanto más diste la distribución con la que se está entrenando de la distribución real menos podremos comparar estas métricas entre sí; por ello, no se pueden probar diferentes estrategias de desbalanceo.

Calidad de las predicciones suaves (soft predictions)

A continuación, nos adentramos en cada una de las métricas que nos ayudan a determinar la calidad de las predicciones suaves, para así conocer su función, ventajas y desventajas.

Cross-entropy

Mide la distancia entre los scores (puntuaciones) y las distribuciones originales.

Ventajas	Desventajas
Es un buen método si nuestro interés reside en tener un buen desempeño global en nuestras puntuaciones.	No evalúa la calidad de la regla de clasificación.

ROC Curves

Realiza las curvas ROC por cada clase para luego calcular el área bajo dichas curvas y así establecer la media o ponderarlas.

Ventajas	Desventajas
Al visualizar las curvas podemos decidir el límite que queremos usar para clasificar.	Requiere un modelo de probabilidad. Su robustez frente a cambios en la distribución de las clases puede ser una desventaja si el dataset está muy desbalanceado.

Precision-recall curves

Se realiza un cálculo del área bajo estas curvas y se promedia o se hace media ponderada.

Ventajas	Desventajas
Al visualizar las curvas podemos decidir el límite que queremos usar para clasificar.	Requiere un modelo de probabilidad.

Cross-entropy

Mide la distancia entre los scores (puntuaciones) y las distribuciones originales.

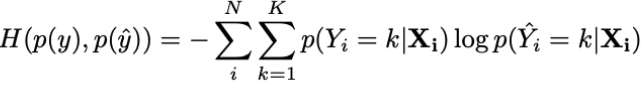
Ventajas
Es un buen método si nuestro interés reside en tener un buen desempeño global en nuestras puntuaciones.

Desventajas
No evalúa la calidad de la regla de clasificación.

---

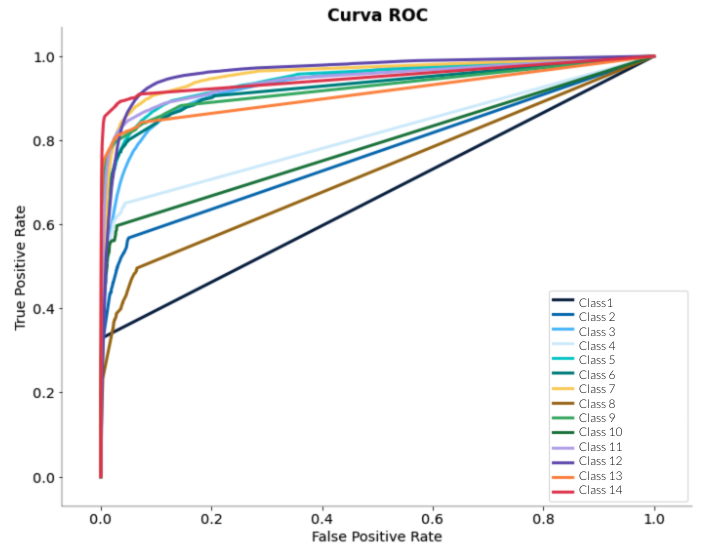
ROC Curves

Realiza las curvas ROC por cada clase para luego calcular el área bajo dichas curvas y así establecer la media o ponderarlas.

Ventajas
Al visualizar las curvas podemos decidir el límite que queremos usar para clasificar.

Desventajas
Requiere un modelo de probabilidad. Su robustez frente a cambios en la distribución de las clases puede ser una desventaja si el dataset está muy desbalanceado.

---

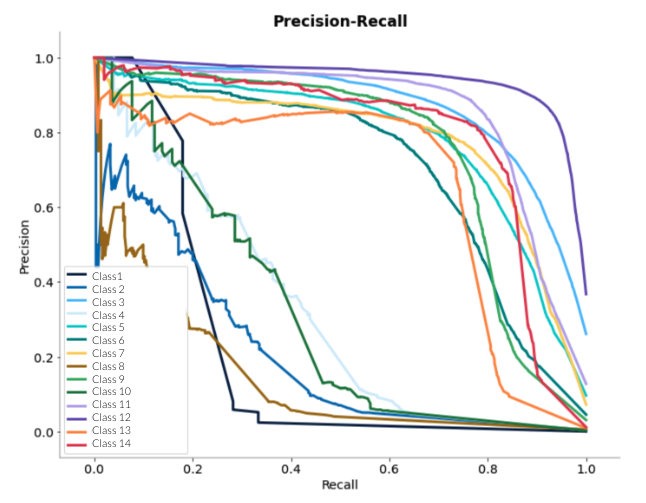
Precision-recall curves

Se realiza un cálculo del área bajo estas curvas y se promedia o se hace media ponderada.

Ventajas
Al visualizar las curvas podemos decidir el límite que queremos usar para clasificar.

Desventajas
Requiere un modelo de probabilidad.

Una vez tenemos una idea más amplia de lo que hace cada métrica, podemos ofrecer una guía con las métricas que nos conviene usar para atajar problemas de clasificación multiclase.

Problemas multilabel: posibles estrategias

En los problemas multilabel las clases no son excluyentes: pueden coexistir. Es decir, una observación puede tener asociada más de una etiqueta. Por ello, la estrategia de uso de métricas difiere. No obstante, existe un problema transversal que implica tanto a los modelos multilabel como a los multiclase: puede existir un desbalance de clases. En el caso multilabel puede ser aún más pronunciado, pues al asignarse más etiquetas a cada observación, si éstas están desbalanceadas, puede afectar en mayor medida a la predicción.

Para intentar resolver estos problemas y explicar los tipos de métricas que pueden ayudarnos a evaluar modelos multilabel, hemos encontrado tres tipos de estrategias en la literatura:^2,3

Ranking-based

Este tipo de estrategia puede servirnos cuando en el caso de uso, además de asignar una etiqueta a una observación, las etiquetas se quieren ordenar en función de su relevancia o probabilidad. En este sentido, este tipo de métricas nos pueden servir cuando la salida del modelo es una lista de etiquetas ordenadas.

Esta estrategia es especialmente apropiada en escenarios extremos de clasificación. También cuando queremos hacer uso de métricas más simples (p.e. Ranking Loss, One-error, Propensity versions…) y es muy útil para crear sistemas de recomendación. Sin embargo, muchos casos de uso no se ajustan al hecho de que la salida del modelo sea en formato ranking

Label-based

Consiste en considerar el problema multilabel como un conjunto de problemas multiclase. El objetivo de esta estrategia consiste en calcular el desempeño en cada una de las clases y después calcular alguna agregación mediante promedios o promedios ponderados.

Nos sirve para evaluar y promediar el rendimiento predictivo de cada categoría como un problema de clasificación binaria; pero, no considera la distribución de etiquetas por observación. Además, las clases no son muestras aleatorias, por lo no siempre será consistente el resultado cuando promediamos las clases.

Example-based

Se trata de un conjunto de métricas que se calculan promediando sobre las observaciones en lugar de sobre las clases. Algunas de estas métricas se basan en teoría de conjuntos (por ejemplo, Jaccard Score o Hamming Loss).

Consiste en calcular, para cada muestra, la proximidad entre los conjuntos de etiquetas predichas y verdaderas. Si bien resuelve el problema de especificidad respecto a las muestras u observaciones, no toma en consideración la especificidad de clases desbalanceadas en problemas de clasificación extremos.

Calculando métricas: Ejercicio con scikit-multilearn

Con la finalidad de complementar nuestra labor de investigación, realizamos un ejercicio práctico que consistió en lo siguiente:

1. Utilizamos el módulo datasets de scikit-learn para generar datos sintéticos correspondientes a un problema de clasificación multilabel. Este módulo está parametrizado, de modo que se puede variar tanto el número de observaciones como el número de etiquetas.
2. Con la ayuda de la librería scikit-multilearn,⁴ y siguiendo el enfoque de Binary Relevance, creamos y entrenamos de manera muy fácil y rápida un conjunto de modelos con diferentes grados de complejidad (por ejemplo, desde un Support Vector Classifier hasta un Gaussian Process Classifier).
3. Para cada modelo candidato, calculamos las métricas para problemas multilabel descritas anteriormente (ranking-based, label-based y sample-based) y las reunimos en forma tabular, para una comparación más fácil. Adicionalmente, también calculamos el tiempo de entrenamiento (fit_time) y el tiempo de inferencia (pred_time) con fines informativos. También, en caso de que la latencia sea importante en nuestro caso de uso.

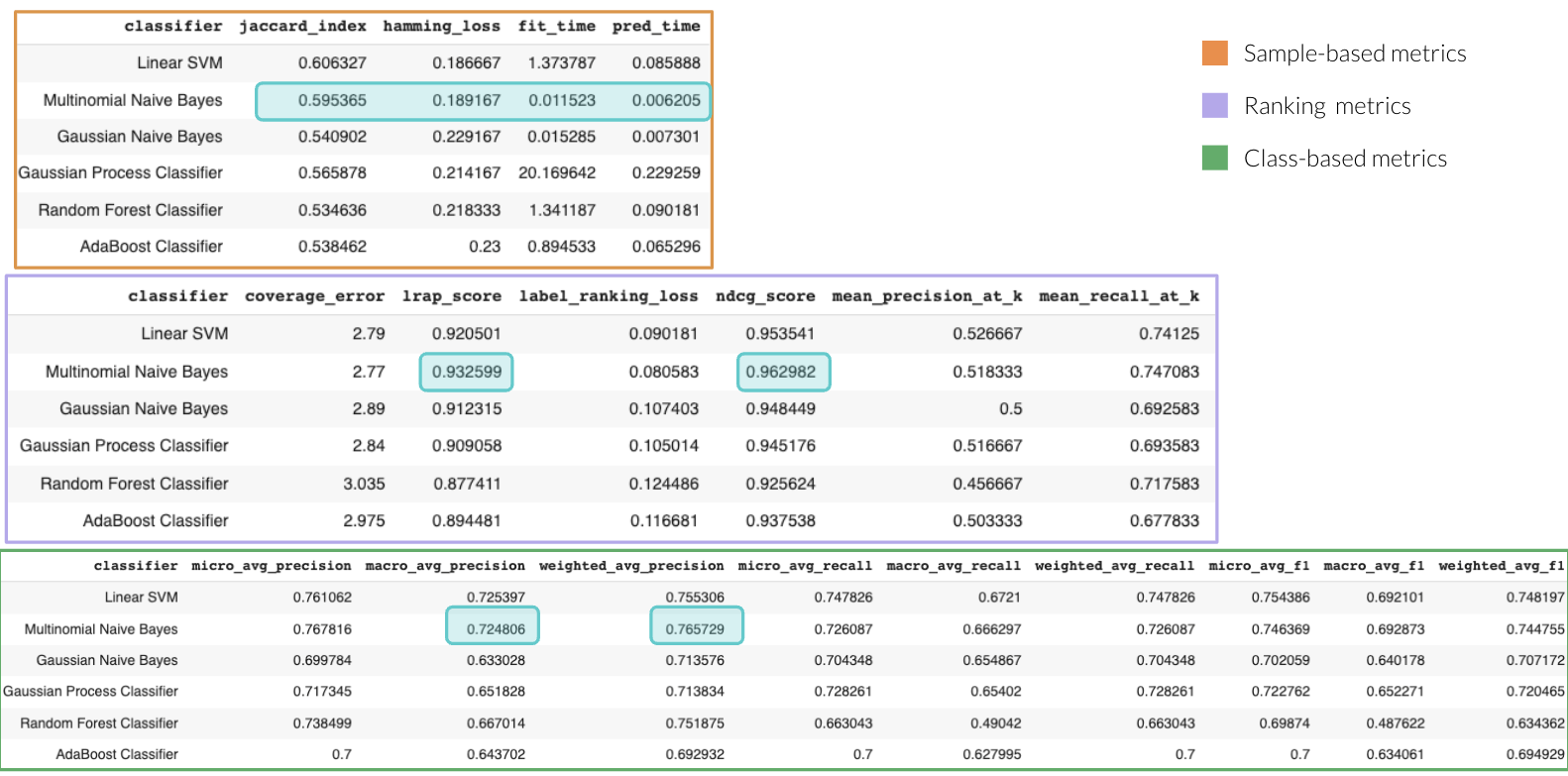
Una vez tenemos todas las métricas calculadas, podemos realizar gráficos en dos dimensiones eligiendo las métricas que nos interese comparar y de esta manera observar cómo es el desempeño de cada modelo fijándonos explícitamente en los trade-offs y poder elegir el que mejor se adecúe a nuestras necesidades.

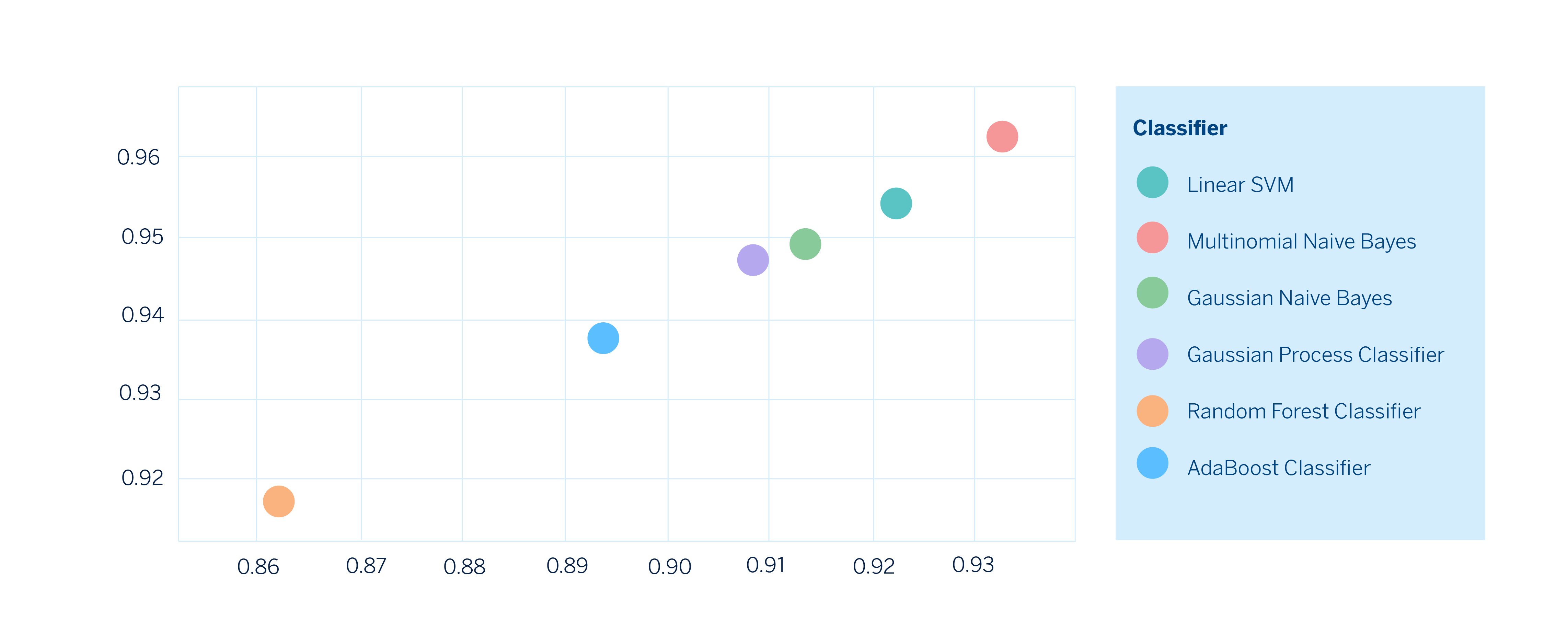
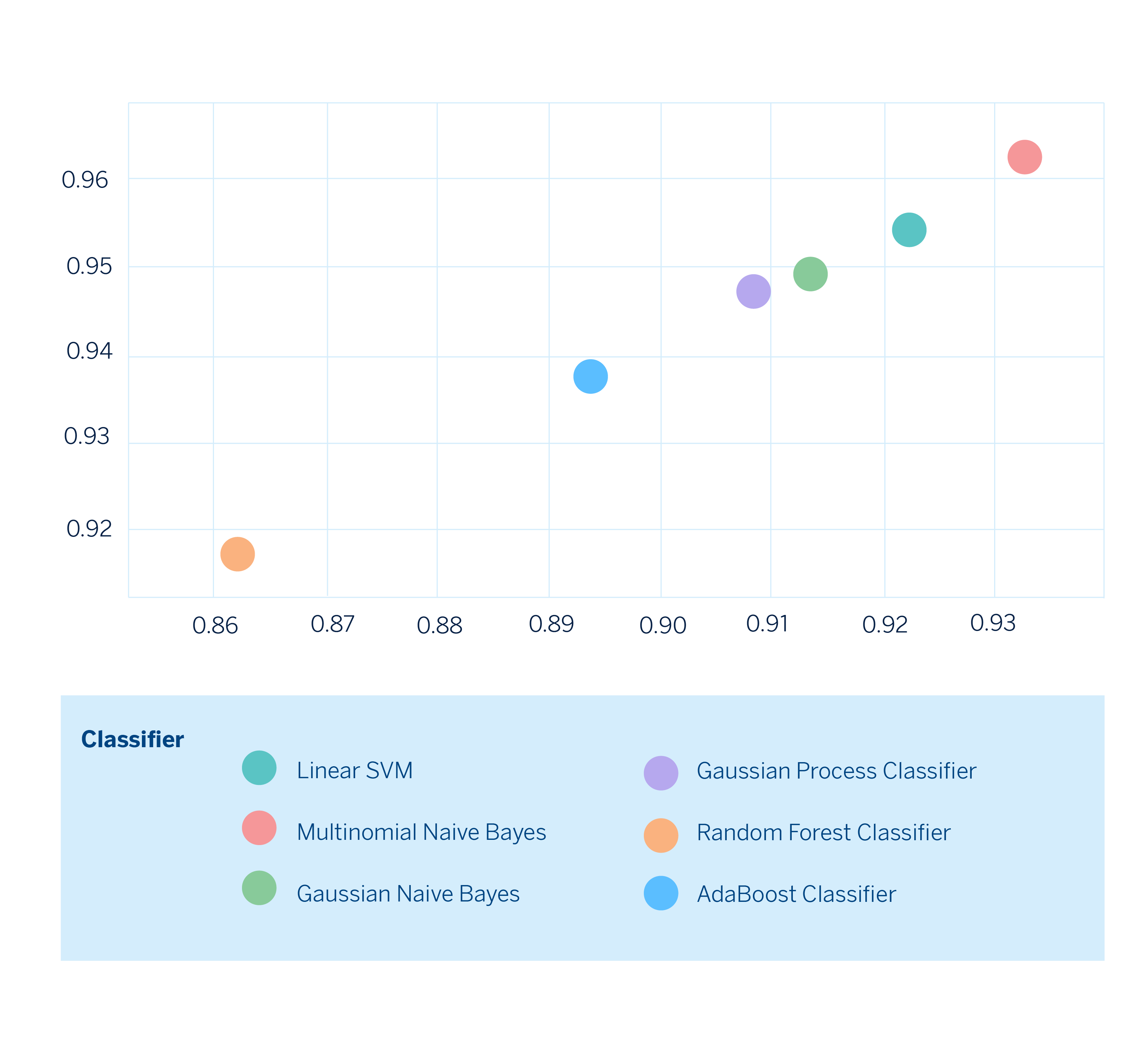
Finalmente, ya podemos elegir el modelo que se adecúe mejor a nuestras necesidades. Bajo este escenario hipotético, el modelo construido con Multinomial Naive Bayes sería el de mejor desempeño en ambas métricas.

Conclusiones

La principal conclusión es clara: no hay métricas buenas ni malas, siempre depende. Depende del caso de uso, depende de la relevancia que tenga el peso de una variable, depende del número de etiquetas que tenga asociada una observación. Sin embargo, hemos conseguido trazar una hoja de ruta para actuar ante los casos multiclase y ampliamos nuestras técnicas en lo que a problemas multilabel se refiere.

Toda esta labor de búsqueda de técnicas aplicables a diferentes casos de uso nos demuestra que la realidad es mucho más compleja, por lo que hay problemas que no pueden solucionarse con las mismas estrategias. Pero, recoger piezas de información que nos ayuden establecer un protocolo de actuación integral frente a problemas de clasificación representa un paso hacia adelante en nuestro recorrido hacia la construcción de experiencias más personalizadas.