
Mercury-explainability para desmitificar algoritmos de caja negra
La explicabilidad busca reducir la distancia entre los usuarios y la complejidad algorítmica, ofreciendo las herramientas necesarias para comprender las decisiones que toman los sistemas de IA.
En este contexto, resulta fundamental establecer un marco de trabajo que nos permita crear algoritmos trazables, auditables e interpretables para que los consumidores de estos sistemas puedan entender cómo operan. Además, se hace patente la necesidad de emplear métodos y técnicas que permitan a los científicos de datos observar el comportamiento algorítmico para así refinar los modelos de aprendizaje automático.
XAI para comprender las decisiones algorítmicas
El concepto de inteligencia artificial explicable (XAI, por sus siglas en inglés, eXplainable AI) nace para comprender la lógica que opera detrás de las decisiones sugeridas por los algoritmos. Surge para reducir la incertidumbre propia del funcionamiento de los modelos de aprendizaje automático, especialmente los de aprendizaje profundo (Deep Learning), y mejorar así nuestro entendimiento de qué procesos se han seguido para llegar a ofrecernos un resultado concreto. Podríamos decir que ayudan a convertir sistemas opacos (cajas negras) en estructuras claras y justificables que nos permitan entender mejor sus decisiones.
La explicabilidad tiene diferentes alcances y beneficios en cuanto al modo en el que sirve a las personas. Por un lado, ayuda a quienes no poseen un bagaje técnico a entender cómo funcionan los algoritmos, lo que incide positivamente en su confianza respecto al uso de estas tecnologías. Esto es especialmente útil dentro de los equipos de negocio: sirve para estrechar su relación con la analítica avanzada y ganar confianza en sus capacidades. En este acercamiento, las unidades de negocio pueden corroborar si un modelo es adecuado para un caso de uso concreto, dándoles la posibilidad de discernir.
Por otro lado, ayuda a los científicos de datos e ingenieros a explicar cómo se comportan los algoritmos en distintos niveles para conjuntos de predicciones y/o predicciones individuales. Esto puede derivar en la detección de posibles errores en el funcionamiento de los modelos, por lo que permite refinarlos, mejorar su rendimiento y así crear algoritmos más robustos.
Existen técnicas de explicabilidad que ayudan a depurar los modelos en la fase de evaluación, lo que permite identificar problemas en los datos como en los propios modelos, para así mejorarlos y entrenarlos de nuevo hasta que puedan validarse como fiables y, entonces, desplegarlos en producción.
La explicabilidad como una metodología de trabajo en BBVA AI Factory
La explicabilidad comprende una serie de técnicas y herramientas que empleamos en AI Factory y que han pasado a formar parte de nuestra metodología de trabajo. Desde una perspectiva clásica, los modelos se entrenaban con datos, dichos modelos realizaban predicciones y posteriormente se realizaba una monitorización de su funcionamiento para luego afinarlos y reentrenarlos.
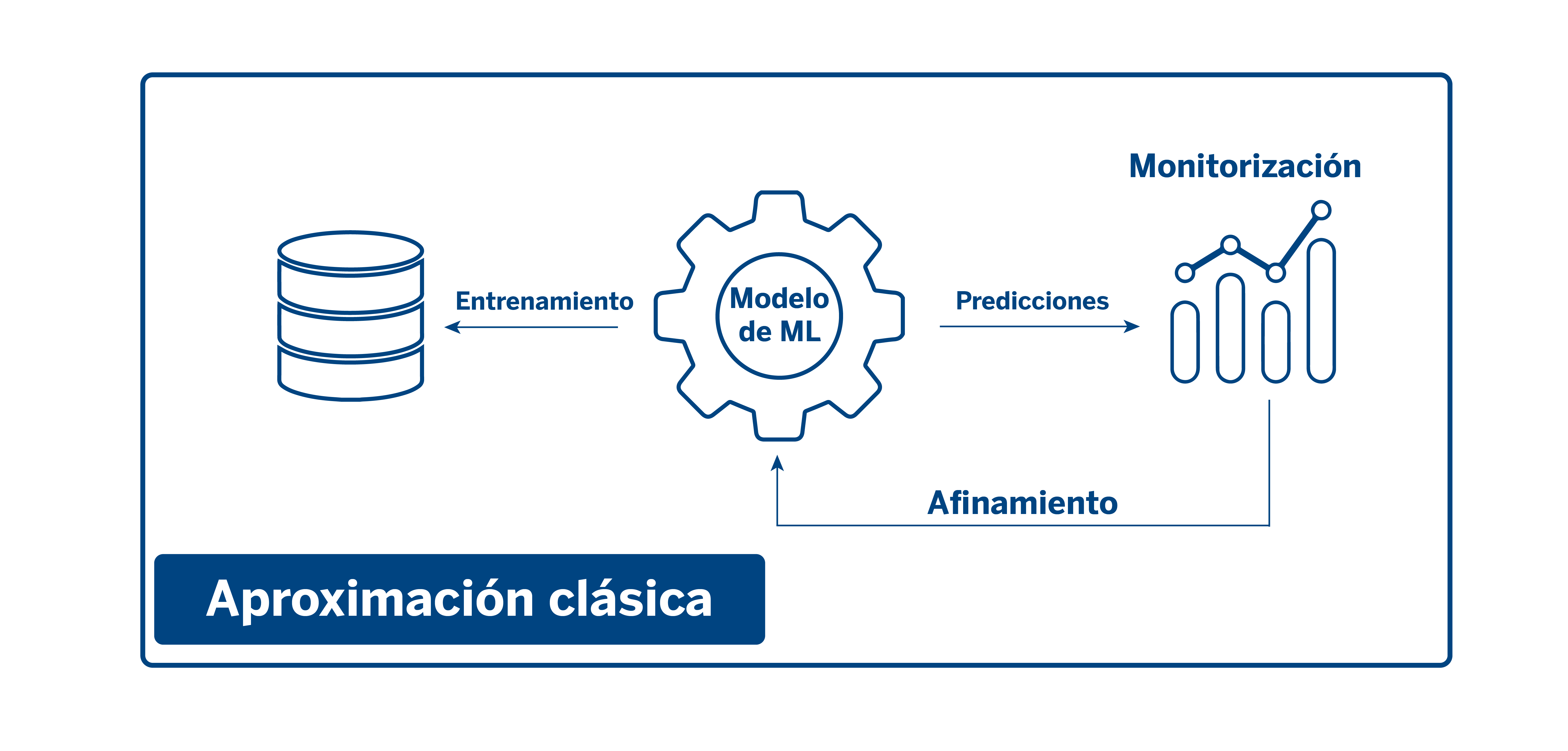
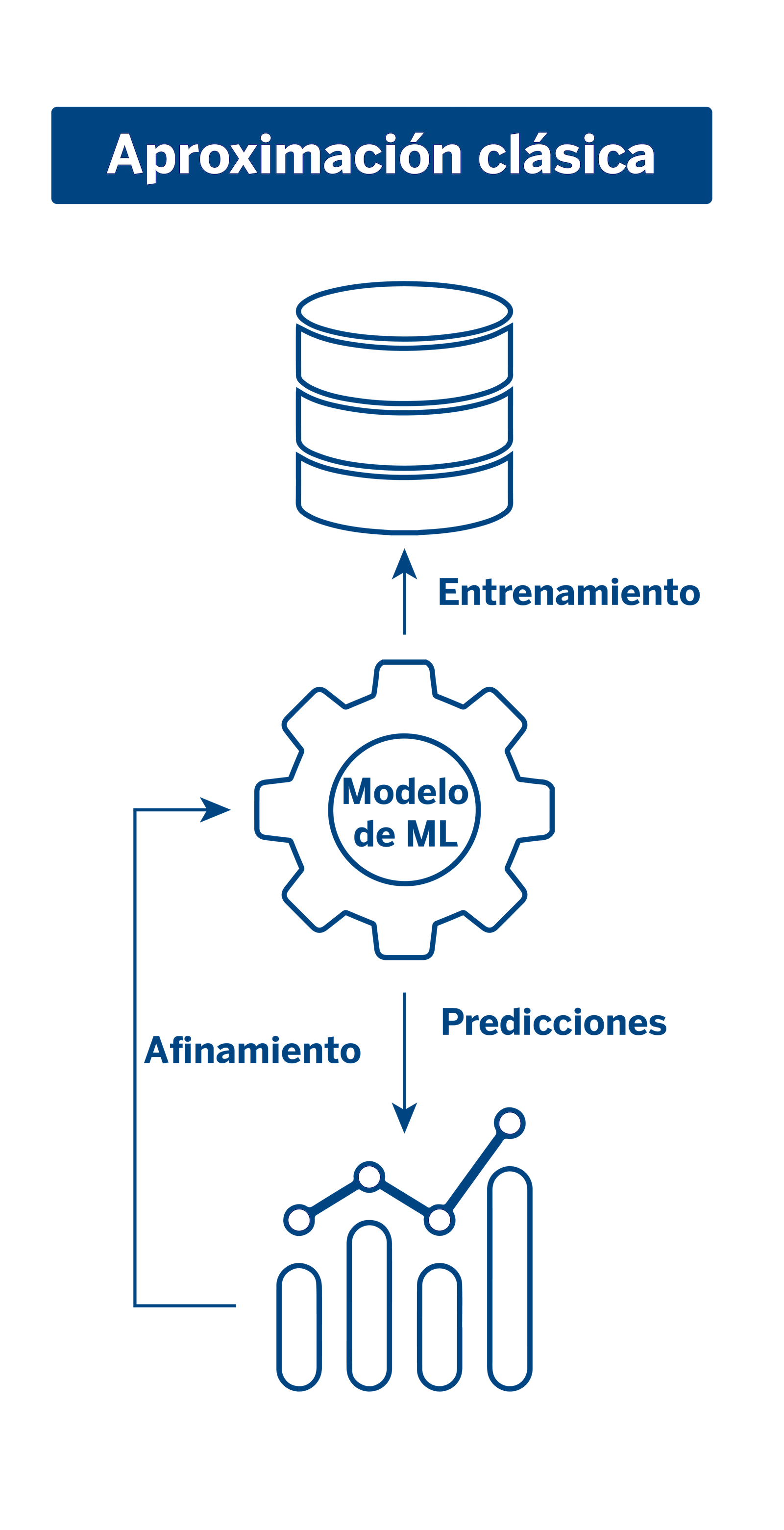
Con la aparición de técnicas de explicabilidad e interpretabilidad, durante el proceso de entrenamiento entra en juego un módulo de explicabilidad a partir del cual se realizan iteraciones tanto en los datos como en los modelos. En este módulo se tienen en cuenta factores como el análisis de las predicciones o la importancia que tienen las distintas variables en el modelo, entre otros elementos que nos ayudan a identificar sesgos o posibles errores antes de desplegarlos en producción.
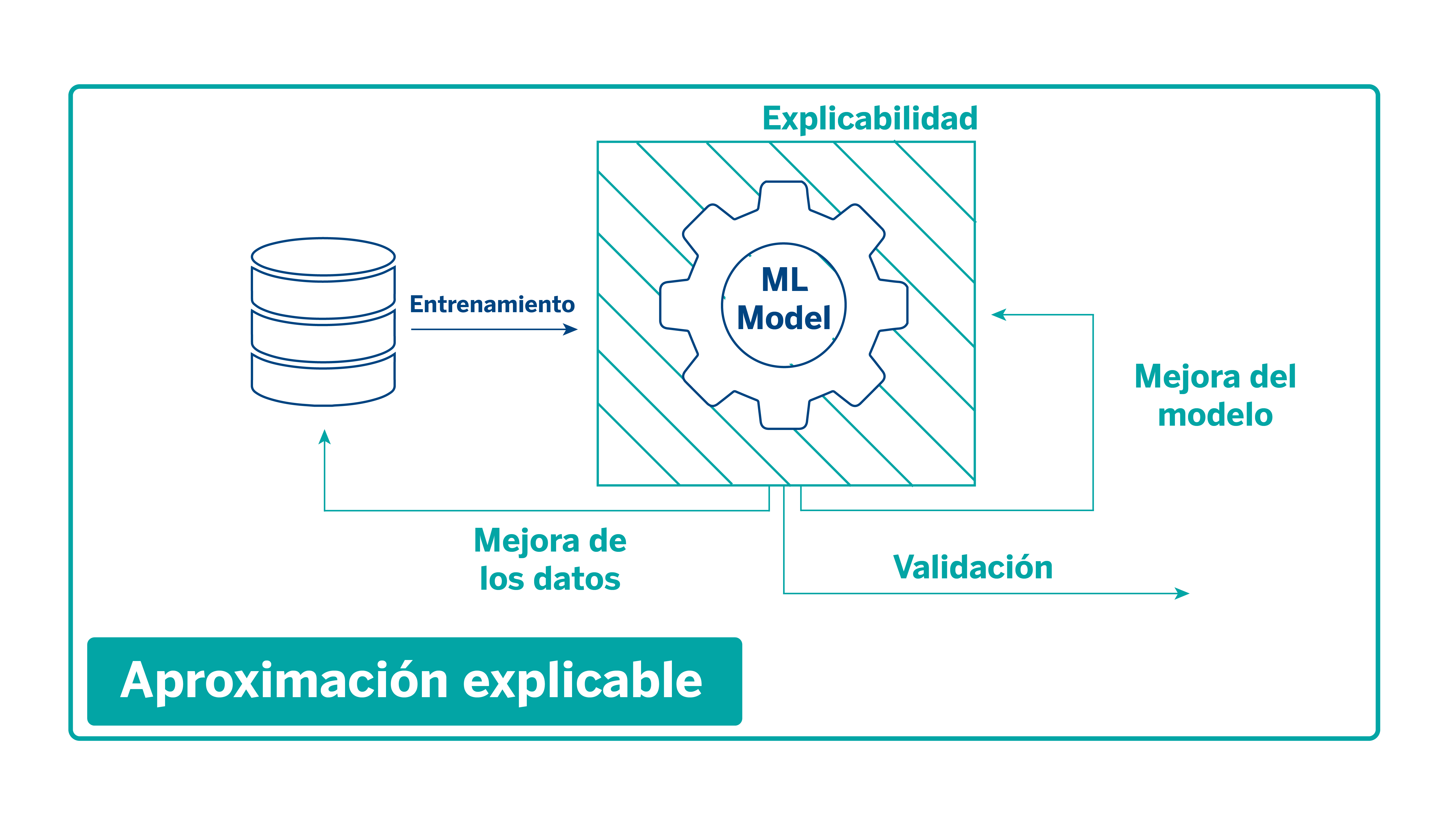
Este módulo lleva el nombre de mercury-explainability, y está disponible en código abierto para cualquier persona que quiera integrar técnicas de explicabilidad en sus modelos.
Mercury-explainability: un módulo de explicabilidad disponible para todos
Como mencionamos en un artículo anterior, desde BBVA AI Factory se desarrolló la librería de código Mercury con el fin de facilitar la reutilización de componentes analíticos dentro de BBVA. Recientemente, parte de esta librería ha sido liberada como open-source para toda la comunidad. Uno de los paquetes liberados, mercury-explainability, contiene componentes que facilitan la explicabilidad de modelos de inteligencia artificial.
Mercury-explainability contiene métodos que no están implementados en otras librerías open-source de explicabilidad con gran adopción como lo son SHAP o LIME. Estos componentes están preparados para funcionar con modelos vistos como cajas negras; es decir, pueden aplicarse a distintos tipos de modelos. Además, algunos de estos componentes pueden ser utilizados para modelos de pyspark.
Algoritmos globales y locales disponibles en mercury-explainability
En la librería podemos encontrar tanto métodos de explicabilidad global como local. Los métodos de explicabilidad global nos proporcionan información de cómo funciona el modelo de forma general, la imagen completa. Estos métodos indican, por ejemplo, qué entradas del modelo suelen ser las más importantes o cómo los cambios en los valores de una entrada del modelo impactan en las predicciones de manera general.
Por otra parte, los métodos de explicabilidad local tratan de explicar la decisión de un modelo para una instancia particular, indicando, por ejemplo, qué entradas en el modelo han tenido el mayor impacto para su predicción.
Métodos de explicabilidad global |
|
| Partial Dependence Plots (PDP) | Este método nos muestra gráficos que demuestran el efecto medio que tiene cambiar uno de los inputs en la predicción del modelo. Así, podemos confirmar cómo varía dicha predicción en función de los datos de entrada. Por ejemplo, si tenemos un modelo que predice la probabilidad de incumplimiento de pago a la hora de conceder un crédito, nos puede ayudar a comprender que nuestro modelo suele disminuir la probabilidad de impago cuando el input del modelo “ingresos mensuales” se incrementa. |
| Accumulated Local Effects (ALE) Plots | Este método es muy parecido a los PDP, ya que muestran cómo las entradas de un modelo afectan a la predicción de manera media. Los ALE Plots suelen ser más fiables en los casos donde existen correlaciones entre diferentes entradas de un modelo. |
| Shuffle Feature Importance | Este método es independiente del modelo, por lo que podemos utilizar cualquier tipo de modelo para adoptarlo. Consiste en estimar la importancia de las diferentes entradas de un modelo de manera general. La importancia de una entrada del modelo se mide realizando un “shuffle” (orden aleatorio) de los valores de esta entrada y se mide cómo impacta en el error del modelo. Si se trata de una entrada importante, el error del modelo subirá por el hecho de haber realizado el shuffle. Sin embargo, si el error del modelo se mantiene, significa que esa entrada tiene poca importancia para el modelo. |
| Clustering Tree Explainer | Cuando aplicamos un algoritmo de clustering como K-Means, normalmente asignamos las instancias de nuestro dataset a clusters o grupos. Sin embargo, a veces es complicado entender el porqué una instancia es asignada a un cluster particular o qué es lo que caracteriza un cluster. Este método está basado en los papers Iterative Mistake Minimization (IMM) y ExKMC: Expanding Explainable K-Means Clustering, y nos ayuda a interpretar los grupos generados por un método de clustering a partir de un árbol de decisión. |
Métodos de explicabilidad global
Partial Dependence Plots (PDP)
Este método nos muestra gráficos que demuestran el efecto medio que tiene cambiar uno de los inputs en la predicción del modelo. Así, podemos confirmar cómo varía dicha predicción en función de los datos de entrada. Por ejemplo, si tenemos un modelo que predice la probabilidad de incumplimiento de pago a la hora de conceder un crédito, nos puede ayudar a comprender que nuestro modelo suele disminuir la probabilidad de impago cuando el input del modelo “ingresos mensuales” se incrementa.
Accumulated Local Effects (ALE) Plots
Este método es muy parecido a los PDP, ya que muestran cómo las entradas de un modelo afectan a la predicción de manera media. Los ALE Plots suelen ser más fiables en los casos donde existen correlaciones entre diferentes entradas de un modelo.
Este método es independiente del modelo, por lo que podemos utilizar cualquier tipo de modelo para adoptarlo. Consiste en estimar la importancia de las diferentes entradas de un modelo de manera general. La importancia de una entrada del modelo se mide realizando un “shuffle” (orden aleatorio) de los valores de esta entrada y se mide cómo impacta en el error del modelo. Si se trata de una entrada importante, el error del modelo subirá por el hecho de haber realizado el shuffle. Sin embargo, si el error del modelo se mantiene, significa que esa entrada tiene poca importancia para el modelo.
Cuando aplicamos un algoritmo de clustering como K-Means, normalmente asignamos las instancias de nuestro dataset a clusters o grupos. Sin embargo, a veces es complicado entender el porqué una instancia es asignada a un cluster particular o qué es lo que caracteriza un cluster. Este método está basado en los papers Iterative Mistake Minimization (IMM) y ExKMC: Expanding Explainable K-Means Clustering, y nos ayuda a interpretar los grupos generados por un método de clustering a partir de un árbol de decisión.
Métodos de explicabilidad local |
|
| Counterfactual Explanations | Este método busca los cambios necesarios en las entradas de una instancia concreta para que la predicción del modelo sea un output predefinido por nosotros en lugar de la predicción actual. Por ejemplo, suponemos de nuevo que tenemos un modelo que predice la probabilidad de impacto a la hora de conceder un crédito, y que para una instancia concreta, el modelo está prediciendo una probabilidad alta. Mediante esta técnica de explicabilidad, podemos encontrar los cambios en las entradas del modelo que son necesarios para que el modelo considere que el cliente tenga una probabilidad baja de impago. Esto podría ser, por ejemplo, que aumente los ingresos mensuales en cierta cantidad, o que disminuya su deuda actual. En mercury-explainability se disponen dos métodos de counterfactuals: CounterFactualExplainerBasic y CounterfactualProtoExplainer. |
| Anchors Explanations (Reglas) | Este método encuentra reglas en los inputs de un modelo que hacen que una predicción se mantenga igual en la mayoría de los casos. Es decir, la regla indica que si se mantienen ciertos valores en un subconjunto de ciertas entradas de un modelo, la predicción del mismo se suele mantener independientemente de los valores en otras entradas. Por ejemplo, tenemos nuestro modelo de predicción de impago de un préstamo, y para un determinado cliente la predicción de impago es alta. Tenemos que para este cliente, las entradas del modelo son:
“IF “deuda actual” > 500 AND “media de ahorro mensual” < 0 THEN Predict "impago" = TRUE with PRECISION 90% AND COVERAGE 10%. |
Métodos de explicabilidad local
Este método busca los cambios necesarios en las entradas de una instancia concreta para que la predicción del modelo sea un output predefinido por nosotros en lugar de la predicción actual. Por ejemplo, suponemos de nuevo que tenemos un modelo que predice la probabilidad de impacto a la hora de conceder un crédito, y que para una instancia concreta, el modelo está prediciendo una probabilidad alta. Mediante esta técnica de explicabilidad, podemos encontrar los cambios en las entradas del modelo que son necesarios para que el modelo considere que el cliente tenga una probabilidad baja de impago. Esto podría ser, por ejemplo, que aumente los ingresos mensuales en cierta cantidad, o que disminuya su deuda actual. En mercury-explainability se disponen dos métodos de counterfactuals: CounterFactualExplainerBasic y CounterfactualProtoExplainer.
Este método encuentra reglas en los inputs de un modelo que hacen que una predicción se mantenga igual en la mayoría de los casos. Es decir, la regla indica que si se mantienen ciertos valores en un subconjunto de ciertas entradas de un modelo, la predicción del mismo se suele mantener independientemente de los valores en otras entradas.
Por ejemplo, tenemos nuestro modelo de predicción de impago de un préstamo, y para un determinado cliente la predicción de impago es alta. Tenemos que para este cliente, las entradas del modelo son:
- ingresos mensuales: 2000
- deuda actual: 650
- media de ahorro mensual: -400
- otros atributos
Una posible “anchor explanation” podría ser:
“IF “deuda actual” > 500 AND “media de ahorro mensual” < 0 THEN Predict "impago" = TRUE with PRECISION 90% AND COVERAGE 10%.
Esto indicaría, que en nuestro dataset cuando la deuda actual es mayor de 500 y la media de ahorro por mes es negativa, el impago se produce en el 90% de los casos y eso cubre un 10% de las instancias de nuestro dataset.
¡Manos a la obra!
Para poner a prueba todo lo que puedes hacer con mercury-explainability, puedes probar algunos de estos métodos explainers en este tutorial.