Equilibrando el peso de las variables en un árbol de decisión

En ocasiones, al modelar el funcionamiento de un proceso en el que participan diferentes variables, nos encontramos con que algunas de ellas dominan sobre las demás, es decir, ciertas variables ejercen mayor influencia que el resto. Supongamos, por ejemplo, procesos con dato declarativo en los que la variable a predecir es, a su vez, informada por el propio usuario. Un ejemplo de este caso podría ser un estimador del precio de una vivienda como una variable continua, esto es, que pueda tomar cualquier valor numérico, y solicitar a su vez esta información en un formulario como rangos de valores, por ejemplo un campo desplegable con diferentes opciones. En este caso cabe esperar que la información declarada describa casi la totalidad de la variable a predecir. El objetivo de utilizar un estimador sobre un dato ya conocido puede ser muy variado: hacer continua una variable discreta, suavizar una variable, detectar errores en la introducción de datos, refinar el dato declarativo para unificar criterios o, simplemente, cumplir con una regulación.

La importancia de una variable se puede calcular de diferentes formas dependiendo del tipo de modelo que se ajuste. Por ejemplo, en una regresión lineal o logística es habitual que esté relacionada con el peso (coeficiente) asociado a cada variable descriptora, mientras que en el caso de los árboles suele estar relacionada con la reducción de la métrica empleada para hacer las divisiones. También existen técnicas agnósticas del modelo; una de las más conocidas es Permutation Feature Importance¹. Esta técnica se suele emplear en modelos ya entrenados, poco interpretables o altamente no lineales y se basa en romper aleatoriamente la relación entre la variable descriptora y la objetivo observando el consecuente decremento en el rendimiento del modelo. En cualquier caso, independientemente de cómo se mida la importancia de una variable en un modelo, el resultado de la medida representa de alguna manera la dependencia entre la salida del modelo y la variable en cuestión.

En un proceso industrializado en el que se utiliza la salida de un modelo para tomar decisiones no suele ser buena práctica depender mucho de pocas variables. Puede, por ejemplo, que esas variables dejen de informarse por fallos técnicos (o que se informen erróneamente) y, en estos casos, la predicción será más o menos fiable en función de la dependencia que tenga con dichas variables. Supongamos el ejemplo anterior, en el que el estimador del precio de la vivienda depende en gran medida del importe declarado. Si en una actualización del formulario se recoge mal dicha variable, por ejemplo por un cambio de formato o el tipo de dato, el estimador proporcionará salidas completamente erróneas.

Otro punto importante es que un modelo que depende altamente de una variable es fácilmente violable y esto puede suponer un problema en un proceso de admisión. Supongamos, sobre el ejemplo anterior, que esta vez el precio estimado de la vivienda proporciona acceso a crédito y que este estimador es altamente dependiente de los ingresos medios declarados por el usuario de forma que a mayor ingreso medio, mayor precio de la vivienda. Si se descubre dicha relación, sería muy sencillo engañar al estimador inflando el valor de ingresos medios, lo que daría lugar a accesos a crédito erróneos.

Por los motivos anteriores, diluir la importancia de las variables en un modelo le aporta robustez ante fallos y ataques. A cambio, generalmente, perdemos en términos de rendimiento.

En el caso de la regresión lineal es posible, en algunos casos, imponer restricciones duras sobre los coeficientes en el proceso de optimización² , así como penalizaciones sobre la magnitud de los coeficientes. Sin embargo, en el caso de los árboles de decisión no se dispone de un procedimiento similar que aplique sobre el propio algoritmo de construcción del modelo.

Una alternativa habitual consiste en introducir ruido aleatorio sobre la variable dominante, tratando de encontrar el equilibrio entre el decremento del poder predictivo y la aportación de esa variable al modelo. También sería posible limitar aleatoriamente el subconjunto de variables candidatas en cada división del árbol, con la desventaja de que deja el ordenamiento de la selección, y por tanto la reducción de la métrica de error, en manos del azar. Otra alternativa sería ordenar esta selección haciendo uso de alguna métrica de error de manera que en los primeros pasos de la decisión solo se pudiesen seleccionar variables que no aportasen demasiado (limitando así las importancias), pero no es un procedimiento sencillo en la práctica porque implica saber desde el inicio cuánto reduce el error cada variable.

Esta última solución, no obstante, suena razonable ya que el hecho de que las variables más importantes entren en juego en las últimas fases de la decisión solventa los problemas mencionados al principio y el modelo resultante no sería tan dependiente de las mismas.

En nuestro caso de uso solo teníamos una variable altamente significativa (~90% en la reducción del error) y el resto de variables con una importancia más o menos balanceada. Así, decidimos aproximar la solución anterior con un procedimiento sencillo que denominamos ExtendedTrees. Consta de dos pasos: en primer lugar, ajustar un árbol de regresión con todas las variables excepto la de mayor importancia. A continuación, extender las hojas del árbol anterior utilizando únicamente la variable que quedó fuera en el paso anterior.

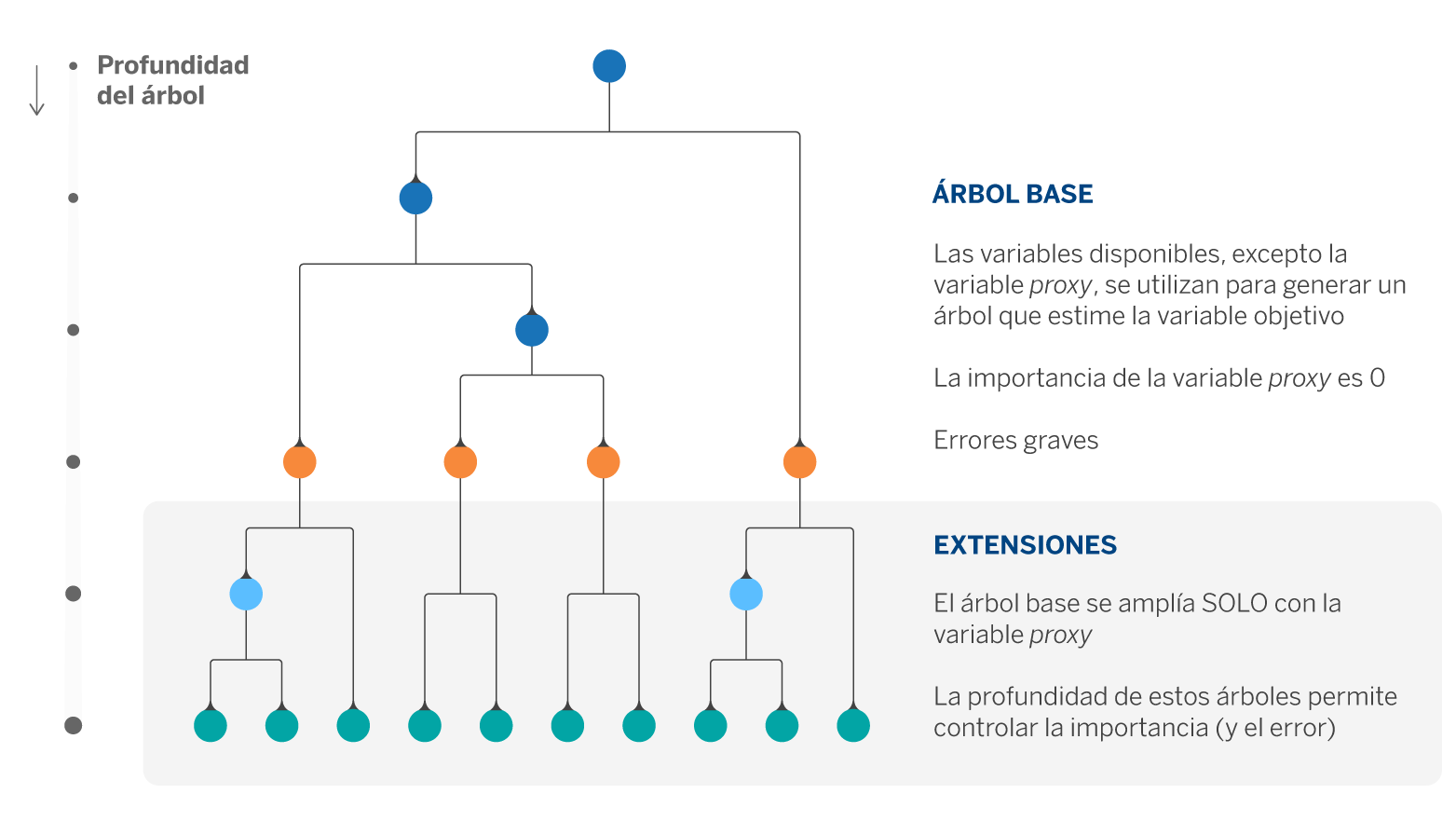
El conjunto de hiperparámetros compuestos por la profundidad del primer árbol y las profundidades de las n extensiones (donde n es el número de hojas del primer árbol) permiten tener el control sobre la aportación de la variable cuya importancia se desea limitar.

Utilizando esta aproximación en nuestro problema conseguimos reducir la importancia de la variable proxy en un ~45% aumentando el error original en un 3%.

Ejercicio con la base de datos de California Housing

Con el objetivo de entender mejor este procedimiento, mostramos un ejemplo de aplicación sobre la base de datos de viviendas de California, (California Housing). Se construyó a partir del censo de viviendas y cada entrada se corresponde con un block group, la unidad geográfica más pequeña para la cual el censo de EE.UU publica información (típicamente engloba a una población de entre 600 y 3.000 personas, similar a la sección censal española).

En total el conjunto de datos consta de 20.640 observaciones, con 8 variables numéricas y la variable objetivo, que son: mediana de ingresos (MedInc), mediana de la antigüedad de las viviendas (HouseAge), media del número de habitaciones (AveRooms) y de dormitorios (AveBedrms), población, ocupación media de las viviendas (AveOccup), latitud y longitud. Así como la variable que queremos predecir, que es el valor mediano de las viviendas de un block group.

En la siguiente figura se muestra la importancia de cada variable descriptora tras entrenar un Decision Tree Regressor (DTR) de profundidad 4 (en azul) y un ExtendedTree (ExT) de profundidad inicial 3 y 2 para las extensiones (en naranja), con el objetivo de estimar el valor mediano de las viviendas de cada block group. En ambos casos se ha empleado la técnica de validación cruzada para obtener los resultados.

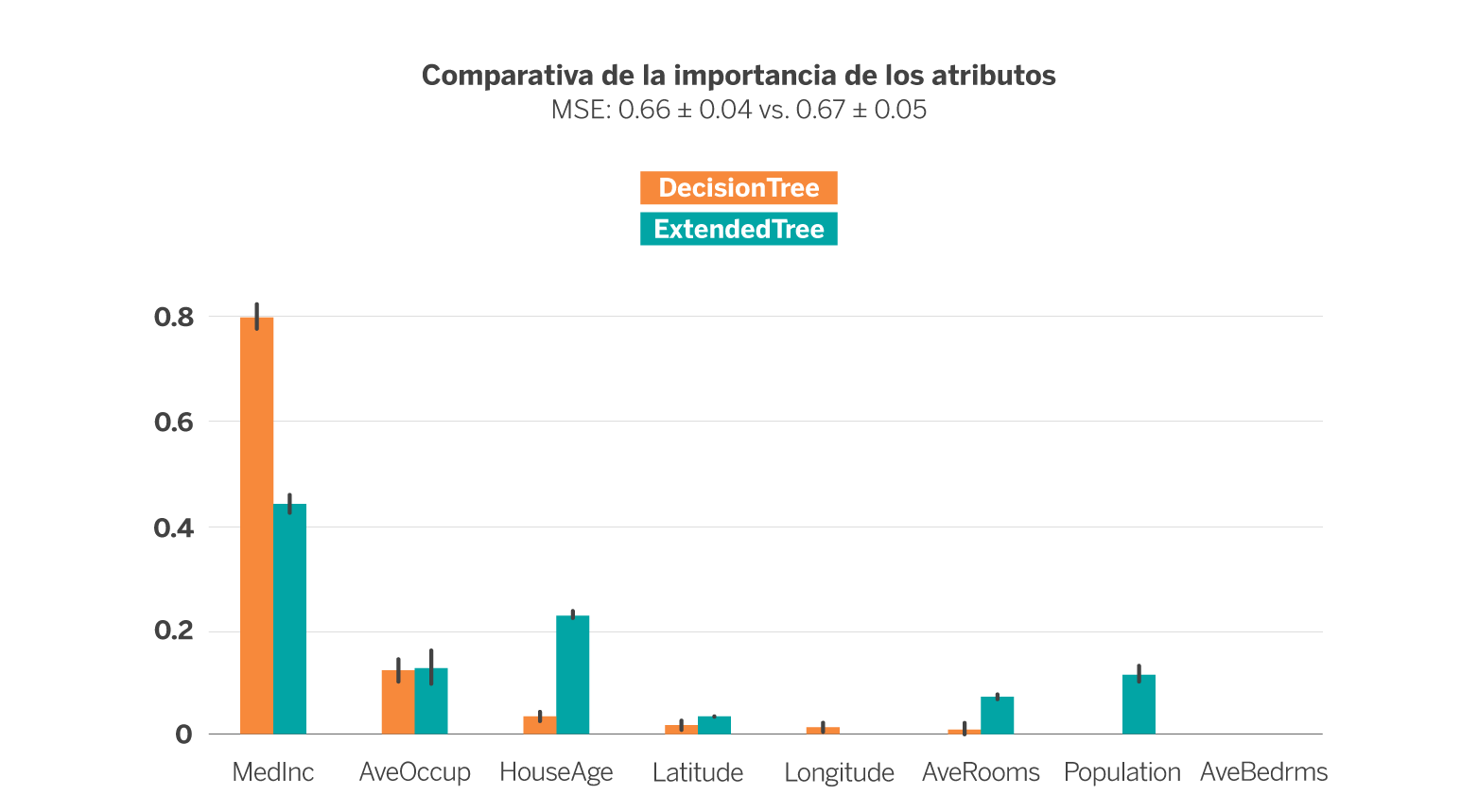
La métrica de error empleada es el Mean Squared Error (MSE), cuyo uso es muy común en la evaluación del rendimiento de modelos de regresión. En este caso, se han configurado ambos modelos de forma que la métrica de error sea lo más similar posible (0.66 ± 0.04 vs. 0.67 ± 0.05), esto es, intentando que ambos estimadores funcionen igual de bien al estimar el valor mediano de las viviendas a partir de las variables disponibles. Dicha configuración da lugar a un árbol de 31 nodos en el caso del DTR y un árbol de 61 nodos en el caso del ExT, es decir, el segundo es mucho más complejo que el primero a igualdad de error.

Si nos fijamos en la importancia de cada variable en cada modelo (representado por la altura de la barra) se observa que el DTR depende en ~80% de la variable MedInc, la siguiente más importante es AvgOccup con algo menos del 20% y el resto de variables apenas influyen en la estimación del modelo. En el caso de ExT, sin embargo, la variable más importante sigue siendo MedInc pero en poco más del 40%, quedando además la importancia más distribuida entre el resto de variables.

Merece la pena destacar el caso de las variables HouseAge, AveRooms y Population (población). Mientras que en el DTR apenas influyen, en el ExT su importancia no es despreciable, es decir, son variables que tienen valor para la estimación del precio pero en el caso del DTR se ven eclipsadas por MedInc. En definitiva, el ExT es capaz de explotar más uniformemente las variables disponibles manteniendo el error a cambio de generar una estructura más compleja.

En conclusión, dependiendo de la naturaleza de los datos, los ExtendedTrees pueden resultar una solución sencilla ante el problema de la alta dependencia en los modelos Decision Tree. Este mecanismo se puede aplicar también en el caso de clasificación. Además, los ExtendedTrees son fáciles de entender, la estructura de su salida es la misma que la de un Decision Tree y permiten controlar, dentro de las posibilidades y mediante las profundidades, la aportación de cada variable en un árbol. Aunque, eso sí, pueden aumentar el error o la complejidad.